
南安电分许技款警 电子工程学院DD School of Electronic Engineering,Xidian University http://see.xidian.edu.cn 场论与复变函数 主讲:徐乐 2014年9月15日星期一
场论与复变函数 主讲:徐乐 2014 年 9 月15日星期一
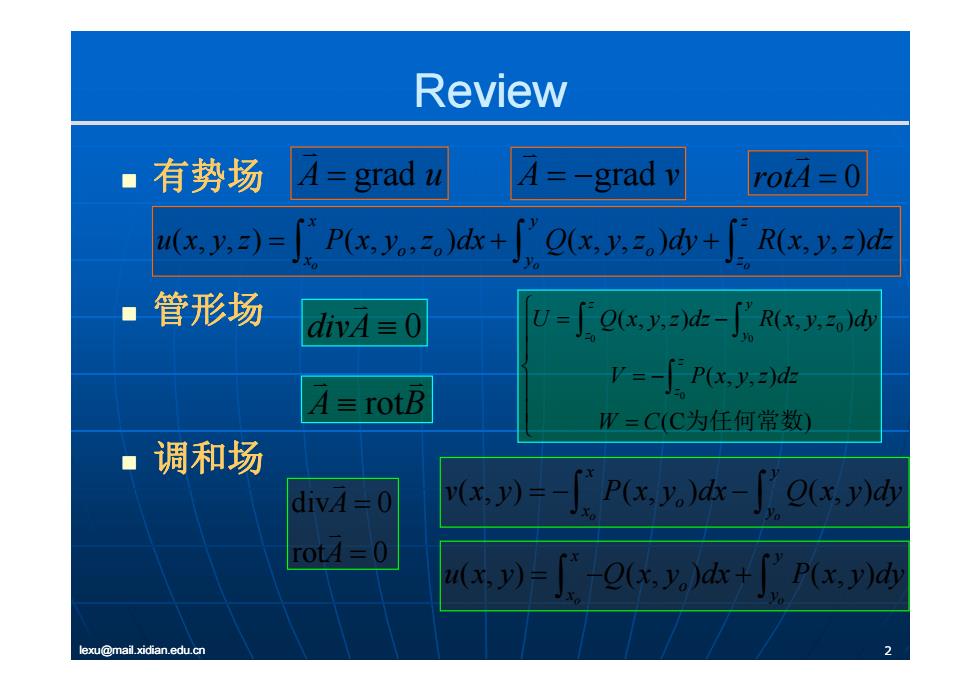
Review ■有势场 A= grad u 4=-grad v rot4=0 (xy,) P(x,)dx+[Q(x.y,=)dy+ R(x,y,)d ◆ 管形场 dia三0 U=∫0xy2d- R(x,y,o)d V=-[P(x.y.)d= A≡rotB W=C(C为任何常数) ·调和场 divA=0 x,)=-「广Px,.)- O(x,y)dy rot4=0 (xy)=广OGxy,)+Pxy) lexu@mail.xidian.edu.cn
Review 有势场 A grad u A grad v rotA 0 有势场 g g (, ,) (, , ) (, , ) (, ,) o oo x yz oo o x y z u x y z Px y z dx Q x y z dy R x y z dz 管形场 o oo y divA 0 0 0 0 (, ,) (, , ) z y z y U Q x y z dz R x y z dy A rotB 0 (, ,) (C ) z z V P x y z dz W C 为任何常数 调和场 W C (C ) 为任何常数 div 0 A (, ) (, ) (, ) x y o v x y P x y dx Q x y dy div 0 rot 0 A A (, ) (, ) (, ) o o o x y y y Q yy (, ) (, ) (, ) x y u x y Q x y dx P x y dy lexu@mail.xidian.edu.cn 2 (, ) (, ) (, ) o o o x y u x y Q x y dx P x y dy
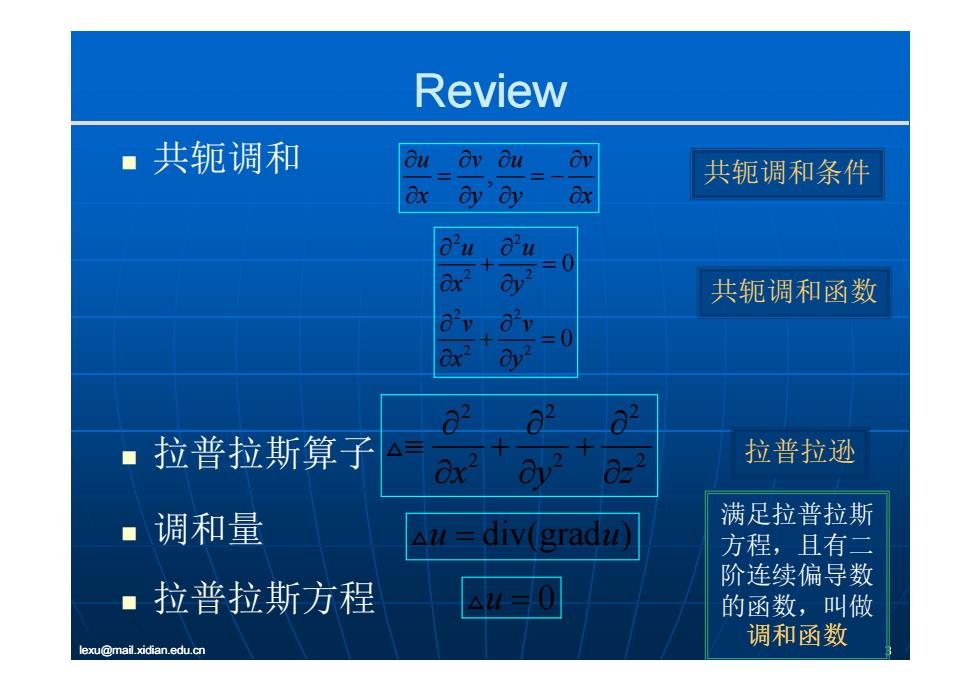
Review ■共轭调和 Ou ov ou ov 共轭调和条件 ox ay'dy dx ouou =0 共轭调和函数 =0 02 O a2 2留 ■拉普拉斯算子 △三 拉普拉逊 调和量 满足拉普拉斯 △u=div(grad 方程,且有二 阶连续偏导数 ■拉普拉斯方程 △u=0 的函数,叫做 调和函数 lexu@mail.xidian.edu.cn
Review 共轭调和 , u vu v 共轭调和条件 x yy x 2 2 0 u u 2 2 2 2 2 2 0 0 x y v v 共轭调和函数 2 2 0 x y 222 拉普拉斯算子 222 xyz 拉普拉逊 满足拉普拉斯 调和量 拉普拉斯 u u div(grad ) 满足拉普拉斯 方程,且有二 阶连续偏导数 lexu@mail.xidian.edu.cn 3 拉普拉斯方程 u 0 阶连续偏导数 的函数,叫做 调和函数

第5讲哈密顿算子及正交曲线坐标系 ■哈密顿算子 ■正交曲线坐标系 lexu@mail.xidian.edu.cn
第5讲 哈密顿算子及 交曲线 标系 正交曲线坐标系 哈密顿算子 正交曲线坐标系 lexu@mail.xidian.edu.cn 4
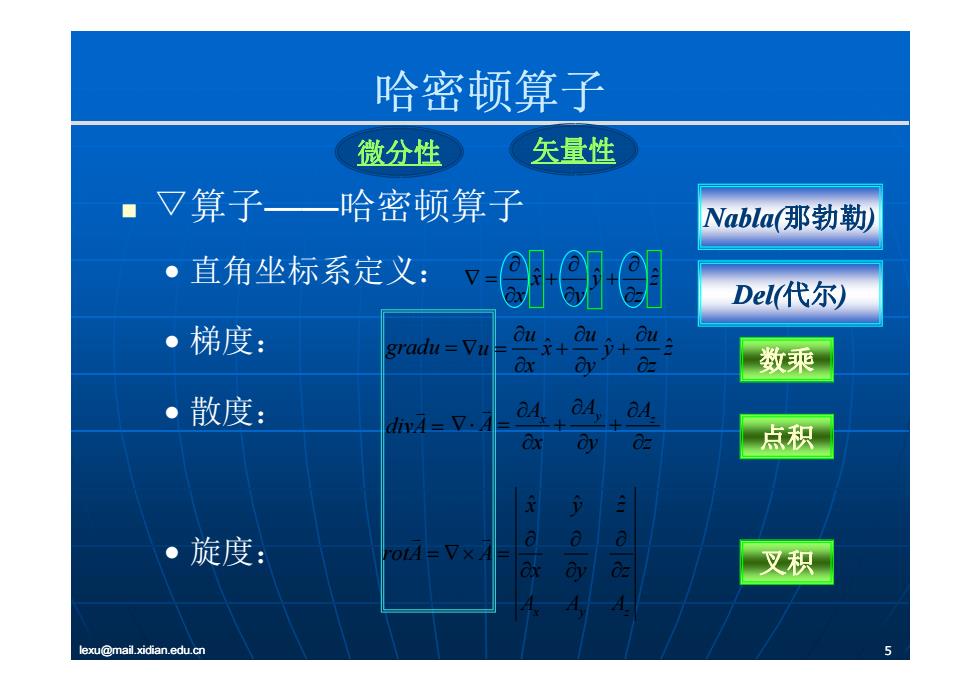
哈密顿算子 微分性 矢量性 ■V算子一哈密顿算子 Nablat那勃勒) ·直角坐标系定义:? Del代尔) ·梯度: gradu Vu 0u+0+ 数乘 ·散度: 4=74 a4,a4 点积 。旋度: ōtdM=7×☒ pa一 叉积 lexu@mail.xidian.edu.cn
哈密顿算子 算 哈密顿算 微分性 矢量性 ▽算子——哈密顿算子 • 直角坐标系定义 Nabla(那勃勒) • 直角坐标系定义: • 梯度: z z y y x x ˆ ˆ ˆ ˆ ˆ ˆ uuu uxyz Del(代尔) • 梯度: gradu • 散度: uxyz x y z x y z A A A A gradu divA 数乘 点 xyz ˆ ˆ ˆ 散度 A x y z divA 点积 xyz A x y z • 旋度: rotA 叉积 lexu@mail.xidian.edu.cn 5 x y z y A A A