
西安在子科枝大拳 电子工学院DD School of Electronic Engineering,Xidian University http://see.xidian.edu.cn edu.cn 场论与复变函数 lexuamail.x 主讲:徐乐 2011年8月30日星期

Review 场论导论 ■矢量场的矢量线 .edu.ch 单值、连续且具 数量场的等值面与等值线 有一阶连续偏导 ■数量场的方向导数与梯度 lexu@mail.xidian.edu.cn

矢量场 。M为天量场中的在意二点亿 矢量场 4=4(M) ·矢量场中分布在各点处的矢量是场点的函数 ·直角坐标系下,矢量场可表示为: A=A(x,y,z)i +A,(x,y,z2)月 +A(民,yz) lexu@mail.xidian.edu.cn
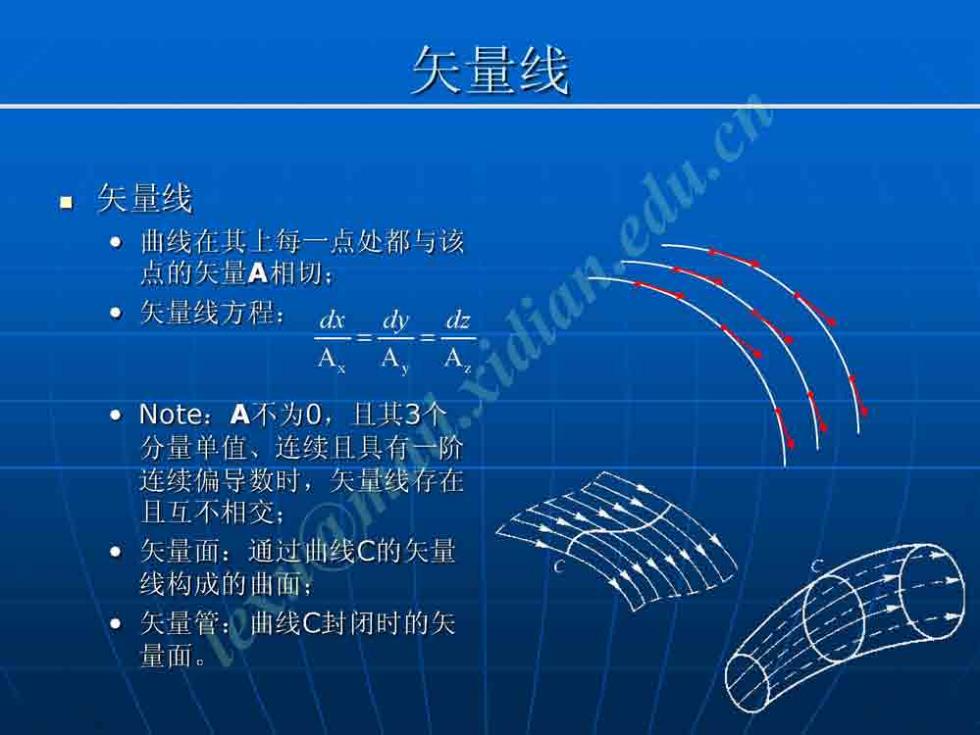
矢量线 ■矢量线 edu.cr 。曲线在其上每一点处都与该 点的东量A相切: 。矢量线方程 d dia dy dz AA、 。Note:A不为0,且其3个 分量单值、连续且具有一阶 连续偏导数时,矢量线存在 且互不相交: 矢量面:通过曲线C的矢量 线构成的曲面 矢量管:曲线C封闭时的矢 量面

等值面 ■等值面 ·在数量场中,使函数取相同数值的所有点组成的曲面 称为该数量场的等值面 ·Notel:函数单值且各连续偏导数不全为0,则等值面必 存在。 Note2:c取遍所有可能值时,这族等值面充满数量场所 在空间,且这族等值面两两互不相交。 ·Note3:数量场中的每一点都有一个等值面通过,且函 数单值,故每一个点均有且仅有一个等值面通过 lexu@mail.xidian.edu.cn