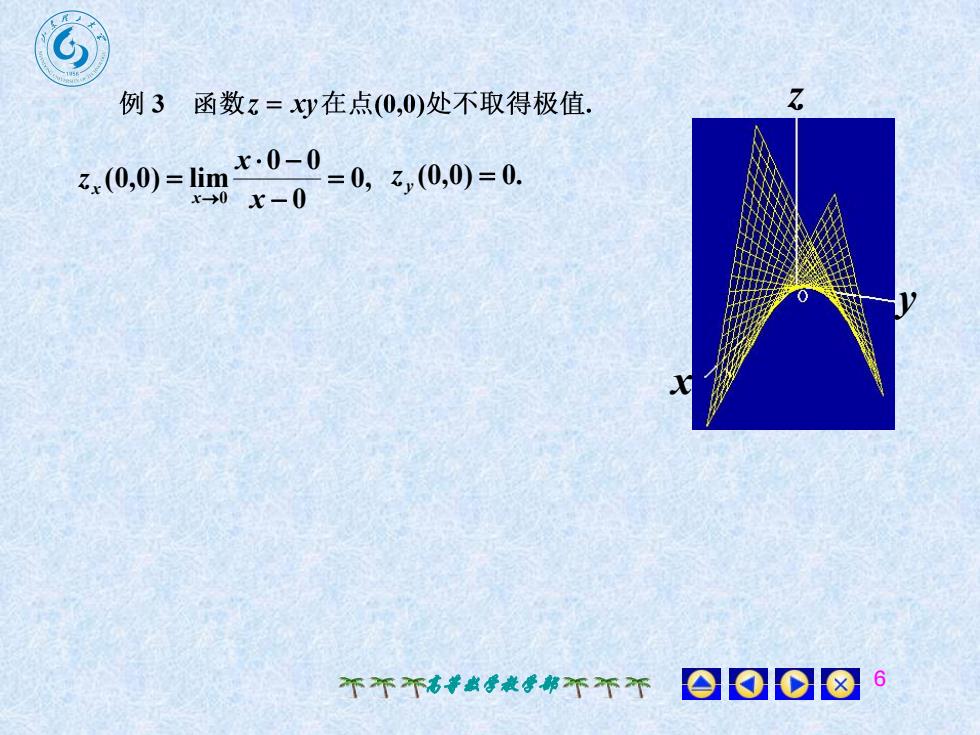
7例 3函数z=xy在点(0,0)处不取得极值x.0-0= 0, z,(0,0) = 0.zx (0,0) = limx-0x-00008个个个高等数学教学部不不个
高等数学教学部 6 x y z 0, 0 0 0 (0,0) lim 0 x x z x x (0,0) 0. y z

62、判定定理定理 1 (必要条件)设函数z= f(x,y)在点(x,J)具有偏导数,且在点(xo,yo)处有极值,则有 f(xo,yo)=0,f,(xo,y)=0.证不妨设z=f(x,y)在点(xs,y.)处有极大值,则对于(xo,y)的某邻域内任何异于(x,y)的点(x,y)都适合不等式f(x,y)<f(x,,yo)故当y= yo, x±x,时,有f(x,yo)<f(xo,Jo),一元函数f(x,Jo)在x=x,处有极大值,f,(xo,yo)=0类似可证f,(xo,yo)=0如果三元函数u= f(x,y,z)在点P(xo,yo,zo)具有偏导数,则它在P(xo,Jo,zo)有极值的必要条件为fx(xo,yo,zo)= 0, f,(xo,yo,zo)= 0, f,(xo, Jo,zo) = 0凡能使一阶偏导数同时为零的点,均称为函数的驻点001018个不高教学教学部不不不
高等数学教学部 7