
第六章大数定律与中心极限定理大数定律6.16.2中心极限定理
6.1 大数定律 6.2 中心极限定理 第六章 大数定律与中心极限定理
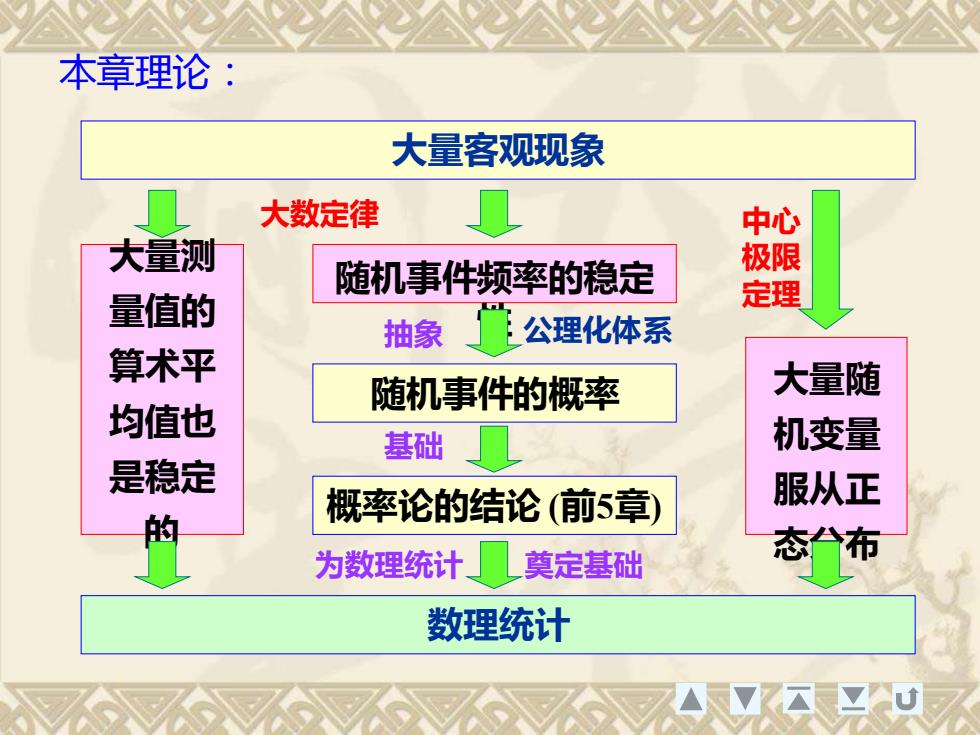
本章理论:大量客观现象大数定律中心大量测极限随机事件频率的稳定定理量值的公理化体系抽象算术平大量随随机事件的概率均值也机变量基础是稳定服从正概率论的结论(前5章)的态台布奠定基础为数理统计数理统计
本章理论: 随机事件的概率 随机事件频率的稳定 性 大量客观现象 概率论的结论 (前5章) 公理化体系 大数定律 抽象 基础 大量测 量值的 算术平 均值也 是稳定 的 大量随 机变量 服从正 态分布 中心 极限 定理 数理统计 为数理统计 奠定基础

大数定律6.1大数定律#是概率论中用来阐明大量随机现象平均结果稳定性和事件频率稳定性的一系列定理
是概率论中用来阐明大量随机现象平均 结果稳定性和事件频率稳定性的一系列定理 大数定律 6.1 大数定律

引理1(切比雪夫不等式)设随机变量X有数学期望EX及方差DX,则对V>0,有DXP((X - EX|≥8)≤(切比雪夫不等式)28或DXP[x-EX|<6}≥1(切比雪夫不等式)证(只就连续型证明)设密度为f(α),则有[x-EX]?P(Ix-EX|≥6)={f(x)dx ≤f(x)dx3[x-EX|≥81x-EX/28DX(**(x- EX)" f(x)dx
引理1 2 1 DX P X − EX − (切比雪夫不等式)设随机变量X 有数学期望EX 或 及方差DX, 则 对 0,有 2 DX P X − EX 证(只就连续型证明)设密度为f (x), 则有 − − = x EX P X EX f (x)d x − − x EX f x x x EX ( )d 2 2 + − (x − EX) f (x)d x 1 2 2 2 DX = (切比雪夫不等式) (切比雪夫不等式)

定理1(切比雪夫大数定律)设X,X.相互独立且分别有数学期望EX,及有公共上界的方差DX,≤K(k=1,2,)作算术平均值Y=1X,则对V>0,有ni=llim P([Y, - EY,|<6}=1n>或Y.-EY.P>0(n→0)(称Y.一EY.依概率收敛于O)宏EEX其中EY=切比雪夫大数定律以严格的数学形式表明:随着n的增大,大量随机变量的算术平均值Y,稳定于它的期望值EY
lim − = 1 → n n n P Y EY 定理1 (切比雪夫大数定律) 设X1 , X2 , . 相互独立且 其中 分别有数学期望EXi 及有公共上界的方差 ( 1,2, ) DX K k i = 1 1 n n i i Y X n = 作算术平均值 = ,则 Y − EY ⎯→0 (n → ) P n n 或 ( 0) 称Y EY n n − 依概率收敛于 1 1 n n i i EY EX n = = 对 0,有 切比雪夫大数定律以严格的数学形式表明:随着n的增 大, 大量随机变量的算术平均值Yn稳定于它的期望值EYn