
第四节 第五章 反常积多 积分限有限 常义积分 被积函数有界 推 反常积分(广义积分)》 一、无穷限的反常积分 二、无界函数的反常积分
二、无界函数的反常积分 第四节 常义积分 积分限有限 被积函数有界 推广 一、无穷限的反常积分 反常积分 (广义积分) 反常积分 第五章
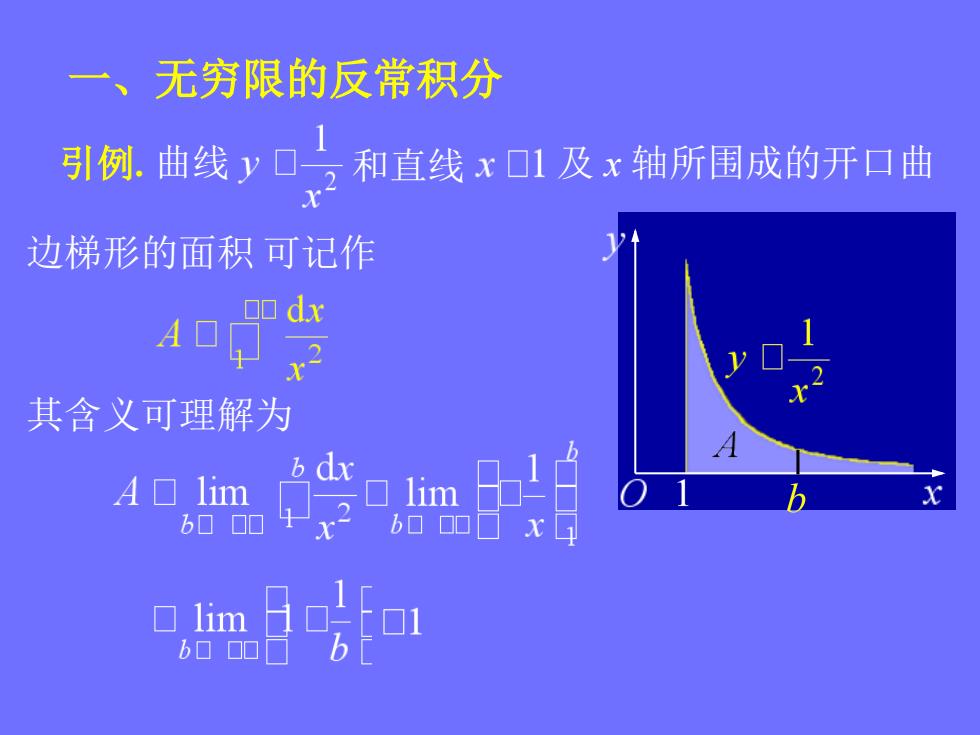
一、无穷限的反常积分 引例.曲线y口二 和直线x口1及x轴所围成的开口曲 边梯形的面积可记作 oo dx A回 其含义可理解为 b dx A▣lim 0 lim b00▣ 0 lim
一、无穷限的反常积分 引例. 曲线 和直线 及 x 轴所围成的开口曲 边梯形的面积 可记作 其含义可理解为

定义1.设f(x)口C[a,口口),取b口a,若 lim (x)dx b00▣ 存在,则称此极限为(x)的无穷限反常积分,记作 f(x)dx口lim f(x)dx b▣口▣ 这时称反常积分f(x)dx收敛,如果上述极限不存在, 就称反常积分 f(x)dx发散 类似地,若f(x)口C(工,b],则定义 ()d lim()dx
定义1. 设 若 存在 , 则称此极限为 f (x) 的无穷限反常积分, 记作 这时称反常积分 收敛 ; 如果上述极限不存在, 就称反常积分 发散 . 类似地 , 若 则定义

若f(x)口C(工,口口),则定义 ()dx Clim ()dxlim ()dx (c为任意取定的常数) 只要有一个极限不存在,就称 f(x)dr发散. 无穷限的反常积分也称为第一类反常积分 说明:上述定义中若出现山山山,并非不定型, 它表明该反常积分发散
则定义 ( c 为任意取定的常数 ) 只要有一个极限不存在 , 就称 发散 . 无穷限的反常积分也称为第一类反常积分. 说明: 上述定义中若出现 并非不定型 , 它表明该反常积分发散

若F(x)是f(x)的原函数,引入记号 F(D)▣limF(x):F(▣)▣limF(x) x0O▣ x0O□ 则有类似牛-莱公式的计算表达式: f(x)dF(x) oF(uF(a) f(x)dx·F(x) b OF(b)□F(I) f(wdF(x)
引入记号 则有类似牛 – 莱公式的计算表达式 :