
3.2 逆矩阵
LOGO 3.2 逆矩阵

·矩阵可逆的定义 。 矩阵可逆的条件 ·逆矩阵的性质
• 矩阵可逆的定义 • 矩阵可逆的条件 • 逆矩阵的性质
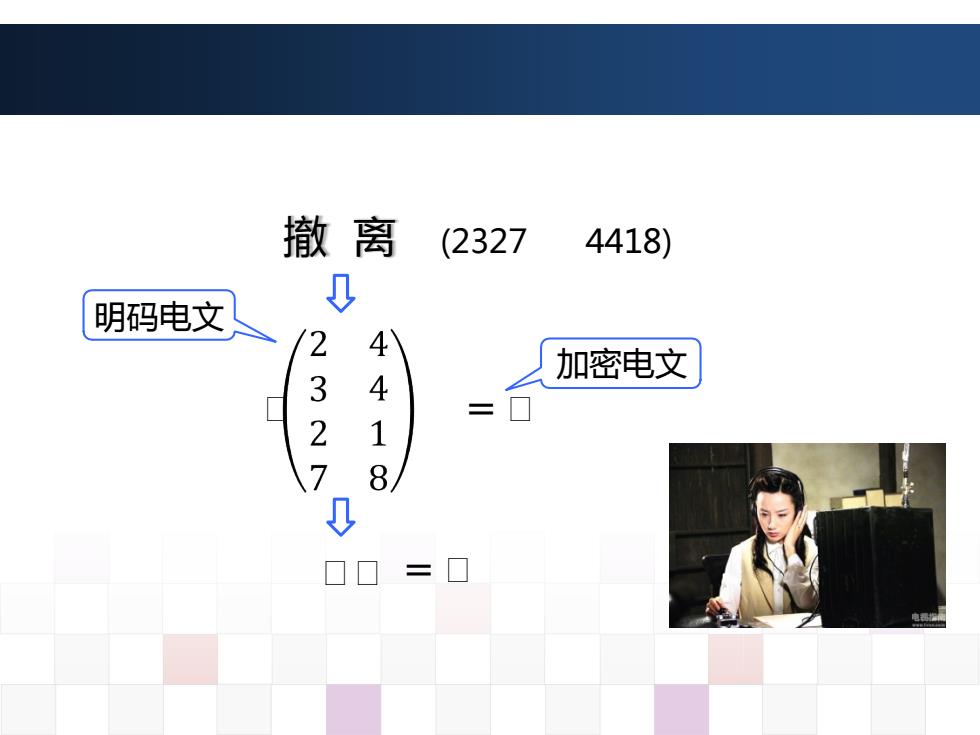
撤离 (2327 4418) 明码电文人 0 2 4 加密电文 N 4 三 8 0 0口 三
撤 离 明码电文 加密电文 (2327 4418) ᵆ = ᵆ ᵆᵆ = ᵆ
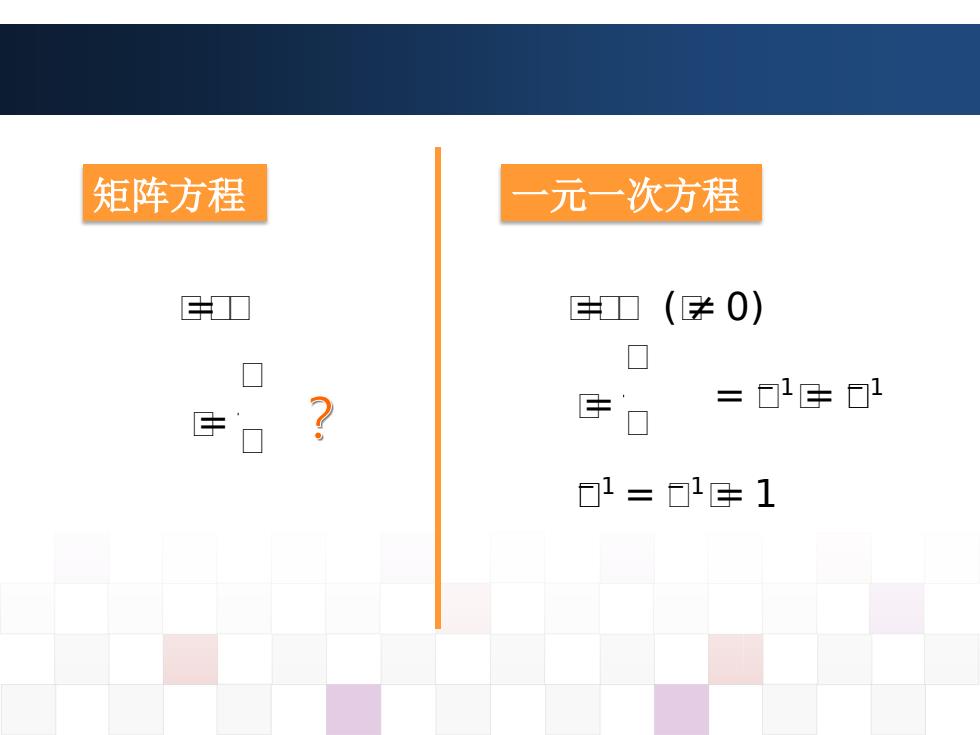
矩阵方程 元一次方程 E口 GH口 (≠0) 口 口 G =1E日1 日1=a1G1
矩阵方程 一元一次方程 ᵆᵆ= ᵆ ᵆ= ᵆ ᵆ ᵆᵆ= ᵆ (ᵆ≠ 0) ᵆ= ᵆ ᵆ = ᵆ− 1ᵆ= ᵆ− 1 ᵆ− 1 = ᵆ− 1ᵆ= 1 ?

一、矩阵可逆的定义 定义3.2.1设A是一个n阶方阵,如果存在一个n阶 方阵B,使得 AB=BA=E 成立,则称矩阵A是可逆的,B称为A的逆矩阵. ·矩阵A与它的逆矩阵互为逆矩阵. ·若矩阵A可逆,则其逆矩阵是唯一的,记作A1
一、矩阵可逆的定义