
2.1消元法与矩阵的初等变 换
LOGO 2.1 消元法与矩阵的初等变 换

·矩阵的定义 矩阵的初等变换 0 线性方程组的基本概念 ·消元法
• 矩阵的定义 • 矩阵的初等变换 • 线性方程组的基本概念 • 消元法
一、矩阵的定义 引例 生活中我们常常会用到矩阵,比如说某工厂 生产3种产品A1,A2,A3,销往5个地方B1,B2, B3,B4,B5,那么每种产品销往每个地方的调运方 案可以通过表格表示为: 0 0 0 0 2.5 3 2 2.3 2 2.5 2.3 2 0 3 3.2 3.2 4 2 3 4 3 1.5 1.5 1 2 1.5 1.5 2 1 2
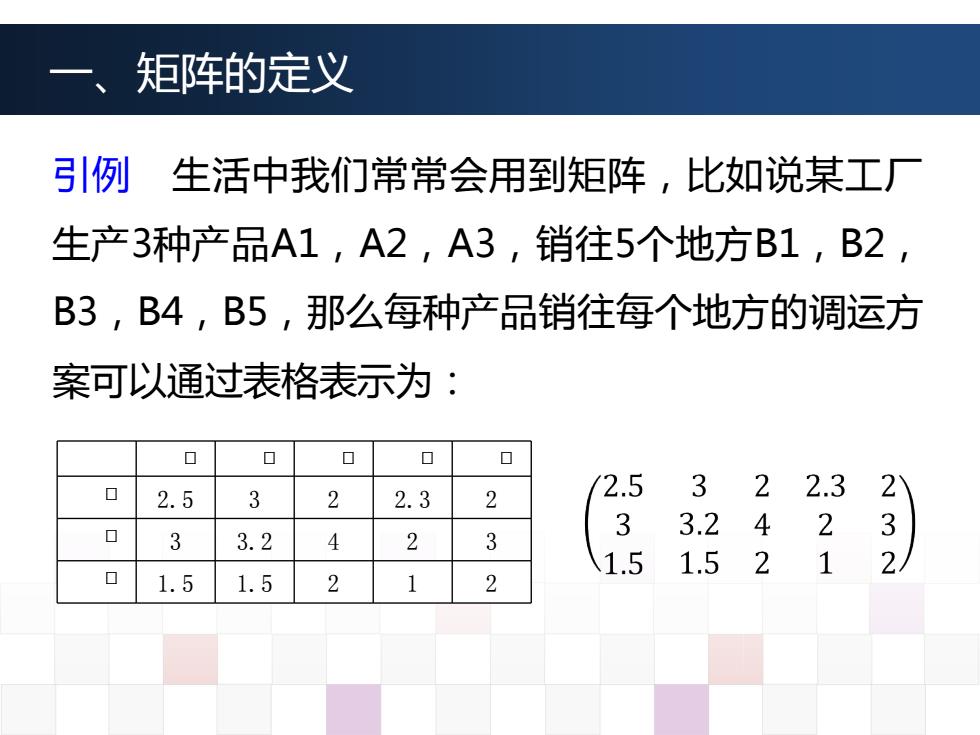
引例 生活中我们常常会用到矩阵,比如说某工厂 生产3种产品A1,A2,A3,销往5个地方B1,B2, B3,B4,B5,那么每种产品销往每个地方的调运方 案可以通过表格表示为: ᵽ ᵽ ᵽ ᵽ ᵽ ᵽ 2.5 3 2 2.3 2 ᵽ 3 3.2 4 2 3 ᵽ 1.5 1.5 2 1 2 一、矩阵的定义

一、矩阵的定义 定义2.1. 1由m×n个数aj(i=1,2,.,m j=1,2,.,n)排成的m行n列的数表 011 012 . 01n 021 022 02n ami 0m2 amn 称为一个m×n矩阵, ·a:称为矩阵第行、第列的元素,称为元素a的 行指标,称为列指标
一、矩阵的定义

一、 矩阵的定义 通常用A,B等表示矩阵,或者也可以用(a),(b) 来表示,如果需要表示矩阵的行数和列数,也可 以写为Amxn或A=(a)mxn: >矩阵和行列式有本质的区别: ·行列式的本质是个数,矩阵是一个数表; ·行列式的行数和列数是相等的,矩阵的行数和列 数可以不相等; ·行列式的符号是!,矩阵的符号是()或者[]
一、矩阵的定义