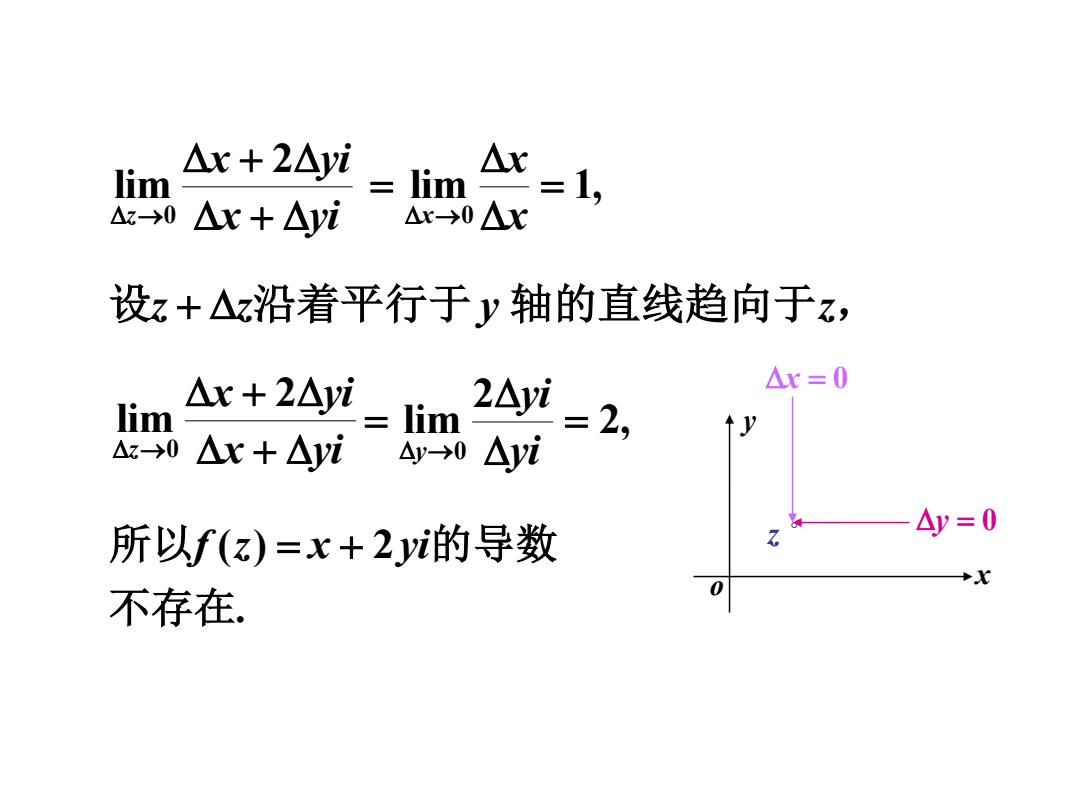
△x+2△yi lim lim 1, △X Az0△x+△yi △x→0△X 设z+△z沿着平行于y轴的直线趋向于z, △x+2△yi 2△i △x=0 lim lim ↑y Az→0△x+△yi △y-→0 △yi 2 所以f(z)=x+2y的导数 △y=0 +X 不存在 0
x y o z y = 0 x yi x yi z + + → 2 lim 0 lim 1, 0 = = → x x x 设z + z沿着平行于 y 轴的直线趋向于z, x = 0 x yi x yi z + + → 2 lim 0 2, 2 lim 0 = = → yi yi y 不存在 所以 的导数 . f (z) = x + 2 yi

·1.1.2可导与连续的关系 ●】 若函数w=f(z)在点z处可导,则f()在 点o处必连续.当w为常数时,连续函数可导. ·证因为 lf()-(]-lim()() z-20 lim (=-z)lim (2)-f(2o) 2→20 2→20 2-20 =0f'(zo)=0 ·知limf(z)=f(2o),故f(z)在点zo处连续
• 1.1.2 可导与连续的关系 • 若函数 在点 处可导,则 在 点 处必连续. 当w为常数时,连续函数可导. • 证 因为 • 知 ,故 在点 处连续. w = f (z) 0 z f (z) 0 z 0 0 0 0 ( ) ( ) lim ( ) ( ) lim ( ) 0 0 z z f z f z f z f z z z z z z z − − − = − → → 0 0 0 ( ) ( ) lim ( ) lim 0 0 z z f z f z z z z z z z − − = − → → = 0 f (z0 ) = 0 lim ( ) ( ) 0 0 f z f z z z = → f (z) 0 z

1.1.3导数运算法则 由于复变函数中导数的定义与一元实变函 数中导数的定义在形式上完全一致,并且复变函 数中的极限运算法测也和实变函数中一样,因而 实变函数中的求导法则都可以不加更改地推广 到复变函数中来,且证明方法也是相同的, 求导公式与法则: ()(c)=0,其中c为复常数 (2)(z")=nz-1,其中n为正整数
由于复变函数中导数的定义与一元实变函 数中导数的定义在形式上完全一致, 并且复变函 数中的极限运算法则也和实变函数中一样, 因而 实变函数中的求导法则都可以不加更改地推广 到复变函数中来, 且证明方法也是相同的. 求导公式与法则: (1) (c) = 0, 其中c为复常数. (2) ( ) , . z n = nzn−1 其中n为正整数 •1.1.3 导数运算法则

(3)[f(z)±g(z)]=f'(a)±g'(z) (4)[f(z)g(z】=f'(z)g(z)+f(z)g'(z. (5) f'(z)gz)-f2)g(). (g(z)≠0) g2(z) (6){fLg(z}=f'(w)g'(z).其中w=g(a) eFomn 其中w=f(z)与z=p(w)是 两个互为反函数的单值函数,且p'(w)≠0
(3) f (z) g(z) = f (z) g(z). (4) f (z)g(z) = f (z)g(z) + f (z)g(z). . ( ( ) 0) ( ) ( ) ( ) ( ) ( ) ( ) ( ) (5) 2 − = g z g z f z g z f z g z g z f z (6) f[g(z)] = f (w)g(z). w = g(z) 其 中 , ( ) 0 , ( ) ( ) ( ) 1 (7) ( ) = = = w w f z z w w f z 两个互为反函数的单值函数 且 其中 与 是

·例3求下列函数的导数. ·(1)f(z)=(2z2+i)5 :- (z≠0) ·解(1) 22 f'(z)=5(2z2+i)44z=20z(2z2+i)4 (2)f"(e)= 41+z2)32z3-2z1+z2)4 =30+-
• 例3 求下列函数的导数. • (1) • (2) • 解 (1) (2) 2 5 f (z) = (2z + i) ( 0) (1 ) ( ) 2 2 4 + = z z z f z f z ( ) = 2 4 2 4 5(2z + i) 4z = 20z(2z + i) 2 3 2 3 2 (1 ) (3 1) z z z = + − 2 3 3 2 4 4 4(1 ) 2 2 (1 ) ( ) z z z z f z z + − + =