
因所求直线与两平面的法向量都垂直 取5=元1×i2= 111 ={4,-1,-3}, 2-13 对称式方程 x-1=y-0 z+2 4 -1-3 x=1+4t 参数方程y=-t z=-2-3t 还有其他方法吗
因所求直线与两平面的法向量都垂直 取 n1 n2 s {4, 1, 3}, 对称式方程 , 3 2 1 0 4 1 x y z 参数方程 . 2 3 1 4 z t y t x t 1 1 1 2 1 3 i j k 还有其他方法吗

法二 x++1=0 (1) 2x①七3z+4=0 (2) (1)+(2)可消去. → 38+4z+5=0 3(1)-(2)可消去z →区+4y-1=0 两个方程中,每一个只有两个变量,解出 共同的变量x.写成比例式,即得对称式方程 1 5 4 x= 1 4
写成比例式, 1 5 4 4 1 3 4 4 y z x 法二 1 0 2 3 4 0 x y z x y z (1) (2) 3 4 5 0 x z 3(1) (2) . 可消去z x y 4 1 0 (1) (2) . 可消去y 两个方程中, 每一个只有两个变量, 共同的变量 即得对称式方程. 解出 x

注.直线的一般方程化为对称式方程(重要) 怎样将直线的一般方程化为对称式方程 有两种方法 ()在直线上找一定点,再求出方向向量, 即写出对称式方程. (2)用代数的消元法化为比例式;
注. 直线的一般方程化为对称式方程 怎样将直线的一般方程 (2) 用代数的消元法化为比例式; 有两种方法 (1) 在直线上找一定点,再求出方向向量, 即写出对称式方程. (重要) 化为对称式方程

例2一直线过点4(2,-3,4),且与y轴垂直相交, 求其方程。 解 因为直线和y轴垂直相交, 所以交点为B(0,-3,0), 取5=BA={2,0,4, 所求直线方程,2=y+3_名-4 2 0 4
解 因为直线和 y 轴垂直相交, 所以交点为 B(0, 3, 0), 取 s BA {2, 0, 4}, 所求直线方程 . 4 4 0 3 2 2 x y z 2 (2, 3,4) . 例 一直线过点A y ,且与 轴垂直相交, 求其方程
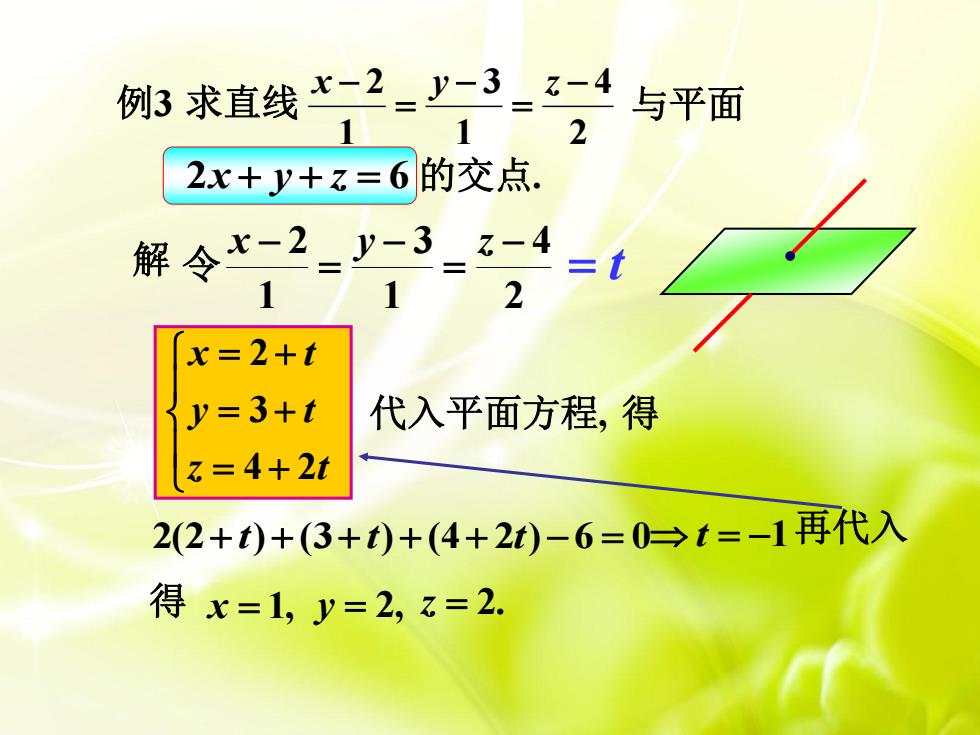
例3求直线七-2 =y-33-4 与平面 1 2 2x+y+z=6的交点. 解令七-2 _y-3z-4 2 =t x=2+t y=3+t 代入平面方程,得 z=4+2t 2(2+)+(3+)+(4+2t)-6=0曰t=-1再代入 得x=1,y=2,=2
2 4 1 3 1 2 x y z 令 2 4 1 3 1 2 x y z 得 2x y z 6 解 z t y t x t 4 2 3 2 2(2 t) (3 t) (4 2t) 6 0 t 1 再代入 代入平面方程, 例3 求直线 与平面 的交点. t 得 x 1, y 2, z 2