
例3计算zdz,其中C为:圆周z=2. 解积分路径的参数方程为 z=2e0(0≤0≤2m), dz=2ieido czdz=22ied6(因为z=2) -4if"(cos+isin)d =0
例3 解 d , : = 2. z z C z C 计算 其中 为 圆周 积分路径的参数方程为 = 2 (0 2π ), i z e d 2 d i z = ie C z dz = 2π 0 2 2 d i ie (因为 z = 2 ) = + 2π 0 4i (cos isin )d = 0

例4求 g-5d.c为以为中心为半 径的正向圆周,n为整数, 解 10 积分路径的参数方程为 =to+reio (0≤8≤2π), x e-dk-gw6 ireie =产e9a0
例4 解 , . d , , ( ) 1 1 0 0 径的正向圆周 为整数 求 为以 为中心 为半 n z C z r z z C n+ − z x y o r 0 z 积分路径的参数方程为 (0 2π), = 0 + i z z re + C − n z z z d ( ) 1 1 0 + + = 2π 0 1 ( 1) d n i n i r e ire d , 2π 0 − = in n e r i
当n=0时, y g-k=rd0=2 0 当n≠0时, +X e=r (cosne-isin ne)de=0; 所以 -k 2πi,n=0, lo, n≠0. 重要结论:积分值与路径圆周的中心和半径无关
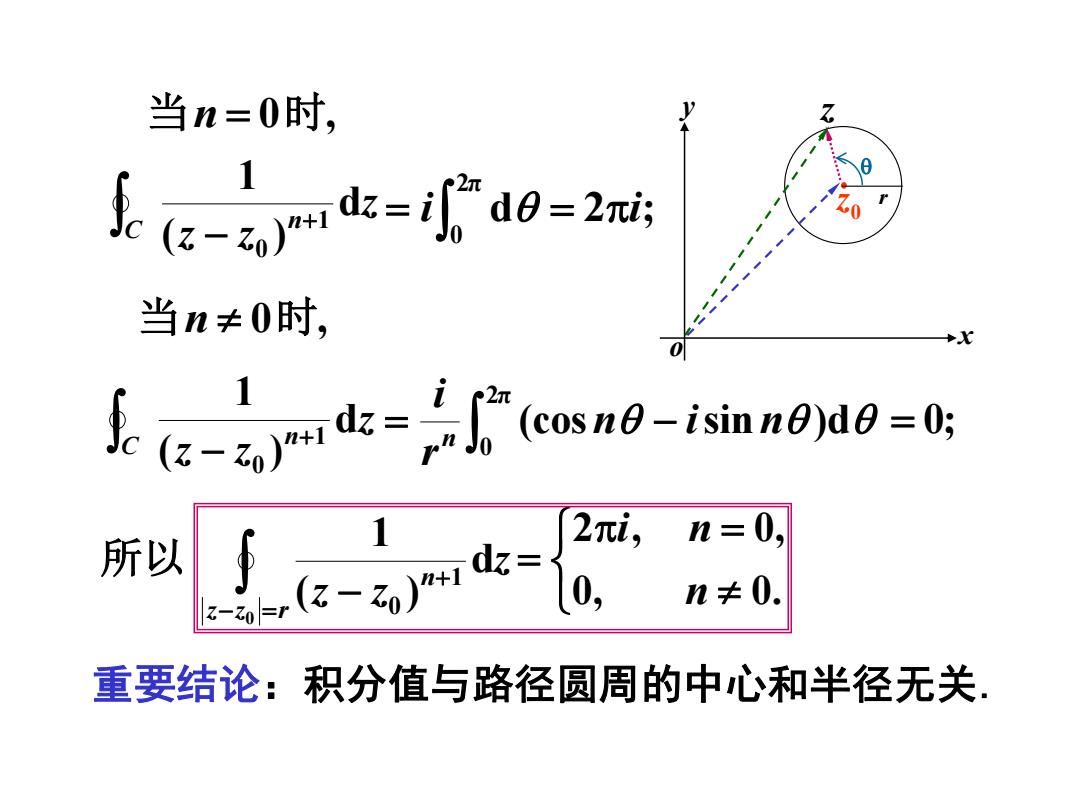
z x y o r 0 z 当n = 0时, + C − n z z z d ( ) 1 1 0 = 2π 0 i d = 2i; 当n 0时, + C − n z z z d ( ) 1 1 0 = − 2π 0 (cos n isin n )d r i n = 0; − = + − z z r n z z z 0 d ( ) 1 1 0 所以 = = 0, 0. 2 , 0, n i n 重要结论:积分值与路径圆周的中心和半径无关

三、积分的性质 复积分与实变函数的定积分有类似的性质, (④cfz)业=-cfz)dz: (2)人faz=k():z(k为常数) (3)∫[fz)±g(z)ldz=Jf(d±[cg(z)dz: (4)设曲线C的长度为L,函数f(z)在C上满足 f(&)≤M,那末[cfz)d≤jcf(zs≤Mm 估值不等式
三、积分的性质 复积分与实变函数的定积分有类似的性质. (1) ( )d ( )d ; = − − C C f z z f z z (2) kf (z)dz k f (z)dz; (k为常数) C C = (3) [ ( ) ( )]d ( )d ( )d ; = C C C f z g z z f z z g z z C C f z M f z z f z s ML C L f z C ( ) , ( )d ( )d . (4) , ( ) 那末 设曲线 的长度为 函数 在 上满足 估 值 不 等 式

性质(4)的证明 因为△zk是zk与zk-1两点之间的距离, △s为这两点之间弧段的长度, 所以 f6x)4≤2f5:)-d≤2f6小△ k=1 k=1 k= 两端取极限得f(z)dz≤Cfzs. 因为∑f5小△≤M∑△=ML, K= k=1 所以[cfz)dz≤f(ds≤ML. [证毕]
性质(4)的证明 , 因为 zk 是 zk 与 zk−1 两点之间的距离 为这两点之间弧段的长度, k s k n k k f z =1 所以 ( ) = n k k k f z 1 ( ) = n k k k f s 1 ( ) 两端取极限得 ( )d ( )d . C C f z z f z s = n k k k f s 1 因为 ( ) = n k k M s 1 = ML, f (z)dz f (z)ds ML. C C 所以 [证毕]