
例1计算∫zd,C:从原点到点3+4i的直线段. 解 直线方程为 [x=3t, y=46, 0≤t≤1, 在C上,z=(3+4i)t, dz =(3+4i)dt, [zdz=[(3+4i)nd-(3+4i)[rdt (3+4i)2 2 又因为czdz=∫c(c+妙)dc+iy)
例1 解 计算 zdz, C :从原点到点3 4i的直线段. C + 直线方程为 0 1, 4 , 3 , = = t y t x t 在C 上, z = (3 + 4i)t, dz = (3 + 4i)dt, d (3 4 ) d 1 0 2 z z = + i t t C (3 4 ) d 1 0 2 = + i t t . 2 (3 4 ) 2 + i = d ( )(d d ) = + + C C 又因为 z z x iy x i y

Szdz =Sxdx-ydy+ifydx+xdy 这两个积分都与路线C无关 所以不论C是怎样从原点连接到点3+4的 曲线, -8
d d d d d = − + + C C C z z x x y y i y x x y 这两个积分都与路线C 无关 , 3 4 曲线 所以不论C 是怎样从原点连接到点 + i的 . 2 (3 4 ) d 2 i z z C + =
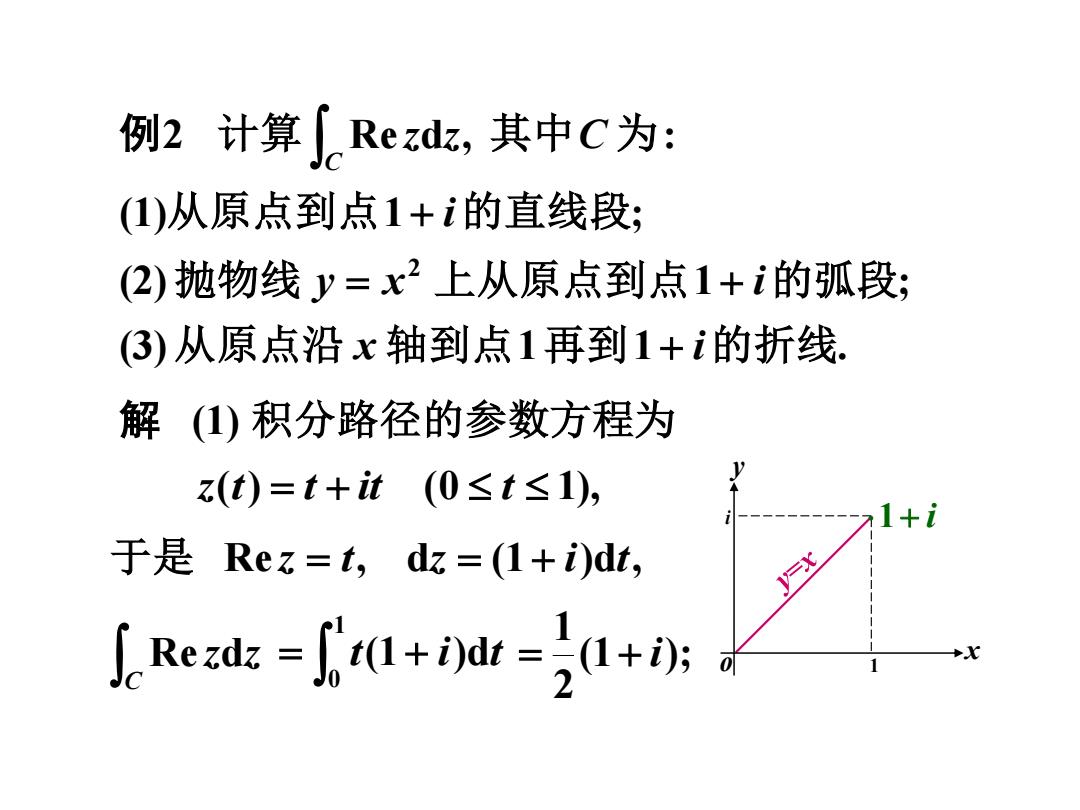
例2计算∫Rezdz,其中C为: (1)从原点到点1+i的直线段; (2)抛物线y=x2上从原点到点1+i的弧段; (3)从原点沿x轴到点1再到1+i的折线. 解(1)积分路径的参数方程为 z(t)=t+it(0≤t≤1), 1+i 于是Rez=t,dz=(1+i)dt, Rezt=tl+i0d=21+0时 x 1
例2 解 (3) 1 1 . (2) 1 ; (1) 1 ; Re d , : 2 从原点沿 轴到点 再到 的折线 抛物线 上从原点到点 的弧段 从原点到点 的直线段 计算 其中 为 x i y x i i z z C C + = + + (1) 积分路径的参数方程为 z(t) = t + it (0 t 1), 于是 Re z = t, dz = (1 + i)dt, C Re zdz = + 1 0 t(1 i)dt (1 ); 2 1 = + i x y o 1+ i 1 i

(2)积分路径的参数方程为 z(t)=t+it2(0≤t≤1), 于是Rez=t,dz=(1+2ti)dt, Readk =f+2i)dr 1 1+i 2i 2 2 y=2 x 0 1
(2) 积分路径的参数方程为 x y o 1+ i 1 i 2 y = x ( ) (0 1), 2 z t = t + it t 于是 Re z = t, dz = (1 + 2ti)dt, C Re zdz = + 1 0 t(1 2it)dt 1 0 3 2 3 2 2 = + t t i ; 3 2 2 1 = + i

(3)积分路径由两段直线段构成 x轴上直线段的参数方程为(t)=t(0≤t≤1), 于是Rez=t,dz=dt, 1到1+i直线段的参数方程为z(t)=1+t(0≤t≤1), 于是Rez=1,dz=idt, [Rezdz-d1id 1+i =x 1 +i. t2 2 x 0
x y o 1+ i 1 i 2 y = x (3) 积分路径由两段直线段构成 x轴上直线段的参数方程为 z(t) = t (0 t 1), 1到1+i直线段的参数方程为 z(t) = 1+ it (0 t 1), 于是 Re z = t, dz = dt, 于是 Re z = 1, dz = idt, C Re zdz= + 1 0 tdt 1 0 1 idt . 2 1 = + i