《线性代数》课程教学课件（PPT讲稿，A）§3.4 分块矩阵

线性代数 第三章祥样三草例1 设0000000-12011-B！AL0012/-14-00-12-1求 AB

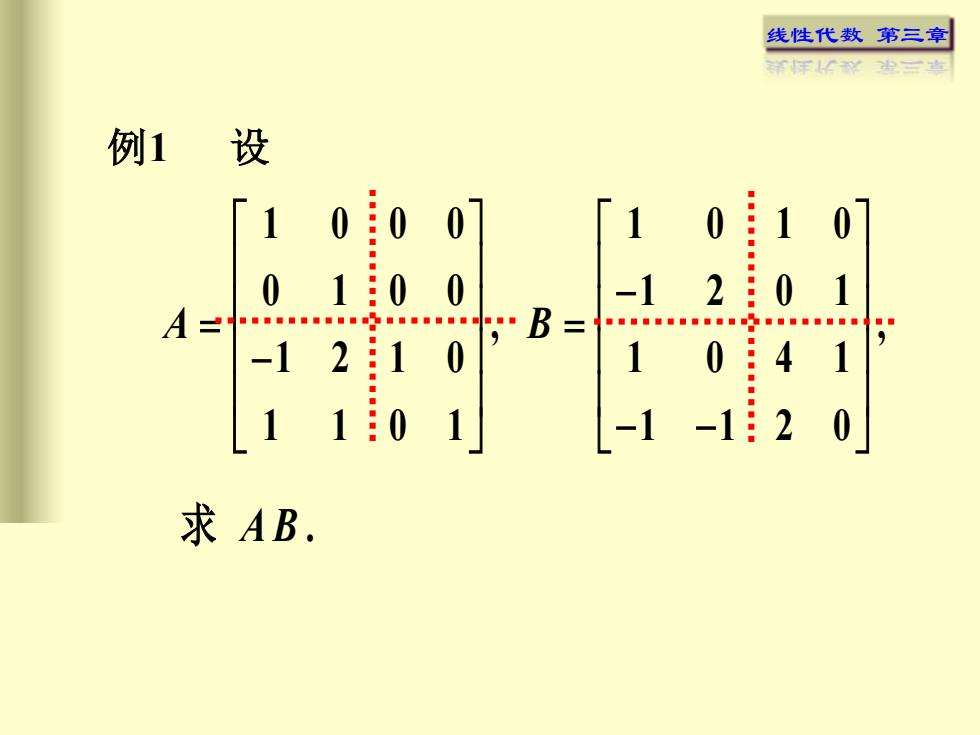
线性代数 第三章 例1 设 1 0 0 0 1 0 1 0 0 1 0 0 1 2 0 1 , , 1 2 1 0 1 0 4 1 1 1 0 1 1 1 2 0 A B         −     = =     −         − − 求 A B

线性代数第三章祥彩光三草解把A,B分块成EEA-12EB :=B21B2201A0

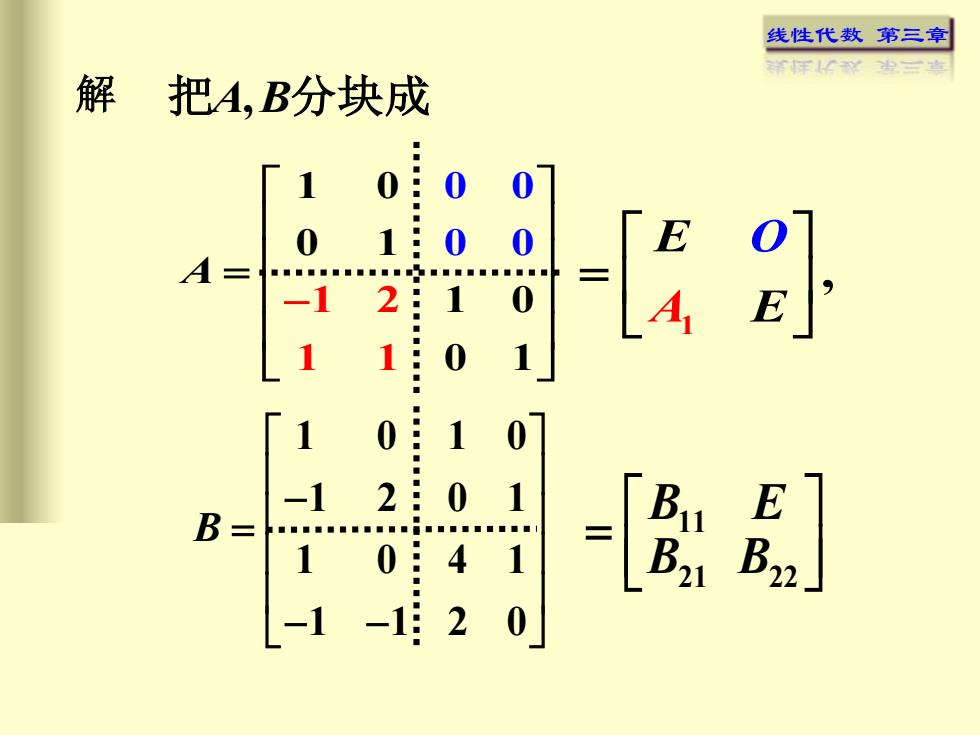
线性代数 第三章 解 把A,B分块成 1 2 1 1 0 0 1 1 0 00 010 0 1 A     =         − 1 , E O A E   =     1 0 1 0 1 2 0 1 1 0 4 1 1 1 2 0 B     − =         − − 11 21 22 B E B B   =    

线性代数第三章祥花光三草E0EB12则 AB=B2EB21AEBu1二A, + B,A,Bu +Ba1220-12.1又A,Bu, + B21 =+2-1-1-24二-1

线性代数 第三章 11 1 21 22 E O B E AB A E B B     =         则 11 1 11 21 1 22 . B E A B B A B   =     + + 1 11 21 1 2 1 0 1 0 1 1 1 2 1 1 A B B       − + = +             − − − 又 2 4 , 1 1   − =     −

线性代数第三章祥样三堂[3312A1A + B22 =31EBr1于是AB =A,Bi + B21A, + B220011-1043-243一1:31-1

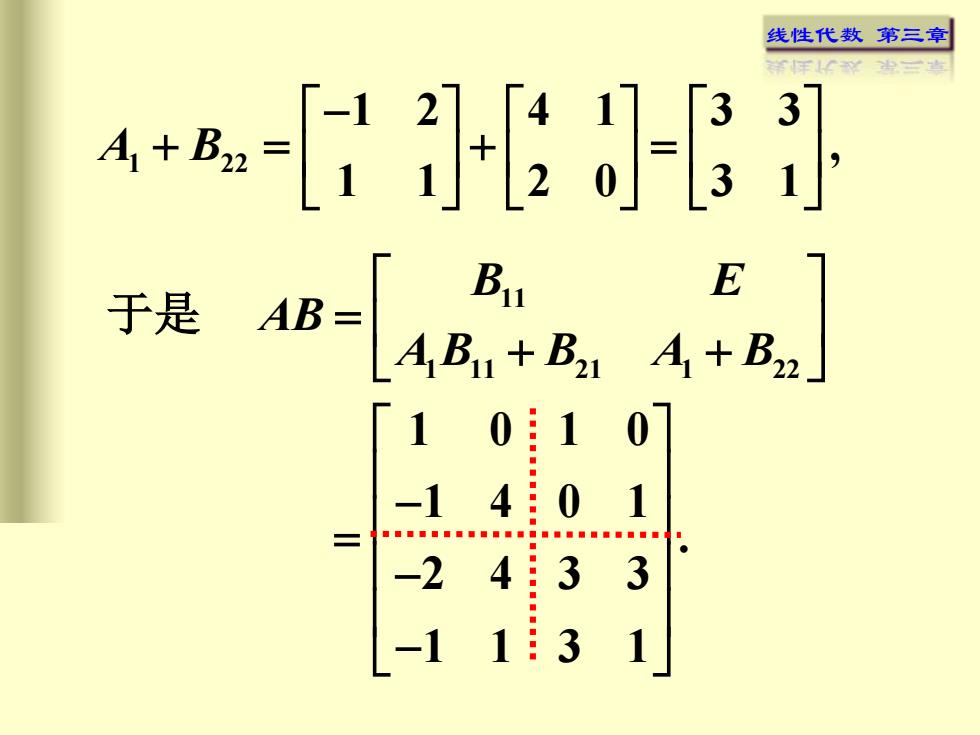
线性代数 第三章 11 1 11 21 1 22 B E AB A B B A B   =     + + 于是 1 0 1 0 1 4 0 1 . 2 4 3 3 1 1 3 1     − =     −     − 1 22 1 2 4 1 3 3 , 1 1 2 0 3 1 A B       − + = + =            

线性代数第三章祥花光三堂三、分块对角矩阵A0A定义形如 A=0的分块矩阵，其中A,为n;阶方阵(i=1,2,,t),称为分块对角矩阵

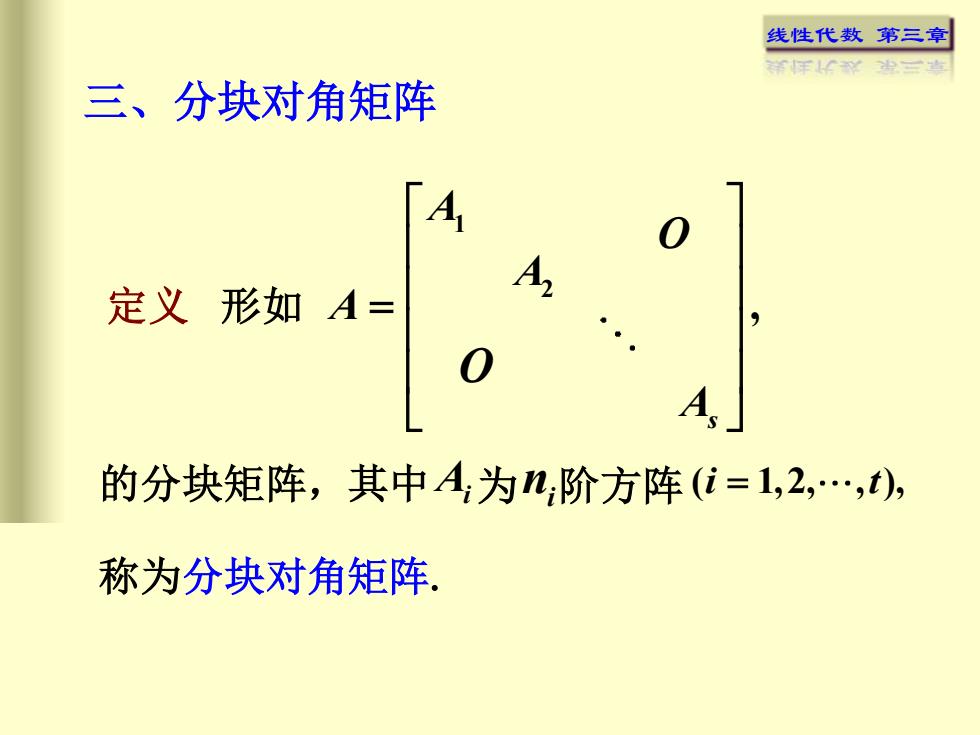
线性代数 第三章 三、分块对角矩阵 的分块矩阵，其中 1 2 , s A A A A       =       O O 称为分块对角矩阵. 形如 Ai 为 ni 阶方阵 ( 1,2, , ), i t = 定义