
§3.2边缘分布 边缘分布均为正态分布的随机变量,其联合分 布不一定是二维正态分布,例如 令(X,)的联合密度函数为 f比,)=1。 -e 2 (1+sinxsiny), 2 显然,(X,Y)不服从正态分布但是 f()= 1-x 2e2,f0)=1e 2 √2 2π 因此边缘分布均为正态分布的随机变量,其联合分 布不一定是二维正态分布
(1 sin sin ), 2π 1 ( , ) ( , ) 2 2 2 f x y e x y X Y x y 令 的联合密度函数为 . 2 1 , ( ) 2 1 ( ) , ( , ) , 2 2 2 2 y Y x X f x e f y e X Y 显 然 不服从正态分布但 是 因此边缘分布均为正态分布的随机变量,其联合分 布不一定是二维正态分布. 边缘分布均为正态分布的随机变量,其联合分 布不一定是二维正态分布, 例如 §3.2 边缘分布

§3.2边缘分布 例设(X,Y)~f(x,y)= e',0<x<y, 0,其它. 求(1)fx(x);(2)P{X+Y≤1. 解当x>0时, fx(x)-[f(x,y)dy-Sedy=e". 当x≤0时, fx(x)=Jf(x,y)dy=0. x>0, 0, 其它
解 f x f x y y X ( ) ( , )d e y x y d f x f x y y X ( ) ( , )d . x e 当 x 0时, 0. 0, . , 0, ( ) 其 它 故 e x f x x X (1) ( ); (2) { 1} . 0, . , 0 , ( , ) ~ ( , ) f x P X Y e x y X Y f x y X y 求 其 它 例 设 当x 0时, §3.2 边缘分布

§3.2边缘分布 (2)P{X+Y≤1} =J∬fx,J)dxdy y=1-x x+y≤1 -fidf"e7dy 1/2 -f le-0-e-Jdx =1+e1-2ei
(2) P{X Y 1} x x y dx e y 1 2 1 0 d e e x x x [ ]d (1 ) 2 1 0 1 2 . 2 1 1 e e f x y x y x y ( , )d d 1 y x O x y y 1 x 1 2 §3.2 边缘分布

§3.2边缘分布 例2一整数N等可能地在1,2,3,.,10十个值中取 一个值.设D=D(N)是能整除N的正整数的个数, F=F(N)是能整除N的素数的个数试写出D和F 的联合分布律并求边缘分布律 解 样本点 12345678910 D 1223242434 F 0111121112 由此得D和F的联合分布律与边缘分布律:
解 1 2 3 4 5 6 7 8 9 10 1 2 2 3 2 4 2 4 3 4 0 1 1 1 1 2 1 1 1 2 例2 . . ( ) . . ( ) , 1,2,3, ,10 的联合分布律并求边缘分布律 是能整除 的素数的个数试写出 和 一个值 设 是能整除 的正整数的个数 一整数 等可能地在 十个值中取 F F N N D F D D N N N 由此得 D和F 的联合分布律与边缘分布律 : 样本点 D F §3.2 边缘分布
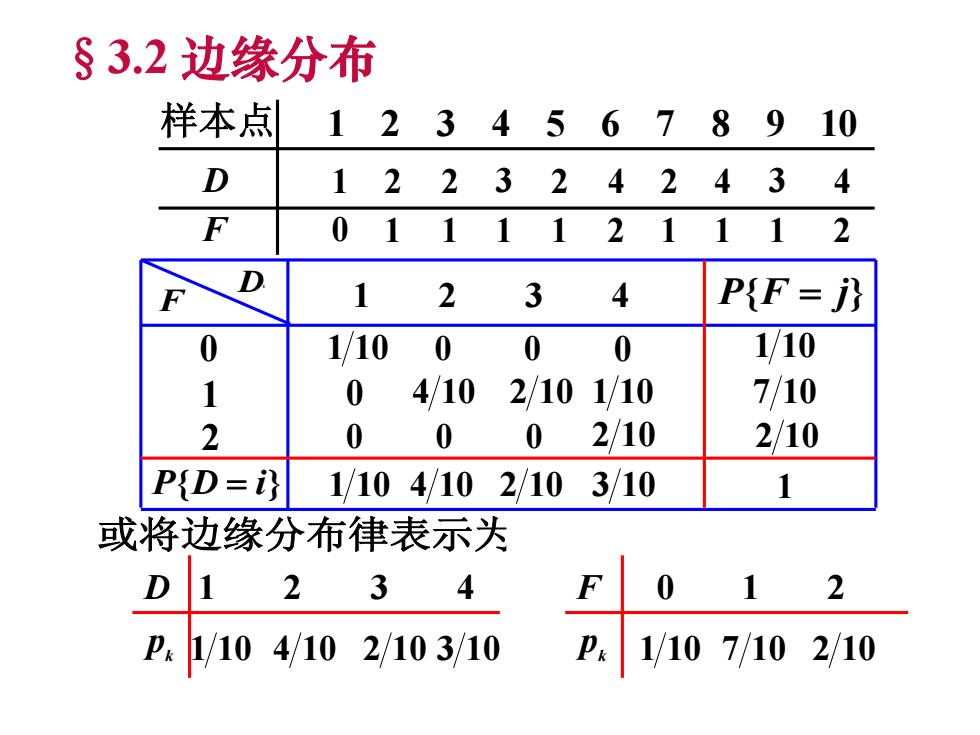
§3.2边缘分布 样本点 12 345678910 D 1223242434 F 01 11121112 D 23 4 P{F=} 0 1/10 0 0 0 1/10 1 04/10 2/101/10 7/10 2 0 0 0 2/10 2/10 P{D=} 1/104/102/103/10 1 或将边缘分布律表示为 23 4 F 2 P.1/104/102/103/10 P.1/107/102/10
D k p 1 2 3 4 1 10 4 10 2 10 3 10 F k p 0 1 2 1 10 7 10 2 10 1 2 3 4 1 10 0 0 0 0 4 10 2 10 1 10 0 0 0 2 10 D F P{F j} 1 10 7 10 2 10 P{D i} 1 10 4 10 2 10 3 10 1 或将边缘分布律表示为 1 2 3 4 5 6 7 8 9 10 1 2 2 3 2 4 2 4 3 4 0 1 1 1 1 2 1 1 1 2 样本点 D F 0 1 2 §3.2 边缘分布