《线性代数》课程教学课件（PPT讲稿，A）§4.3 非齐次线性方程组

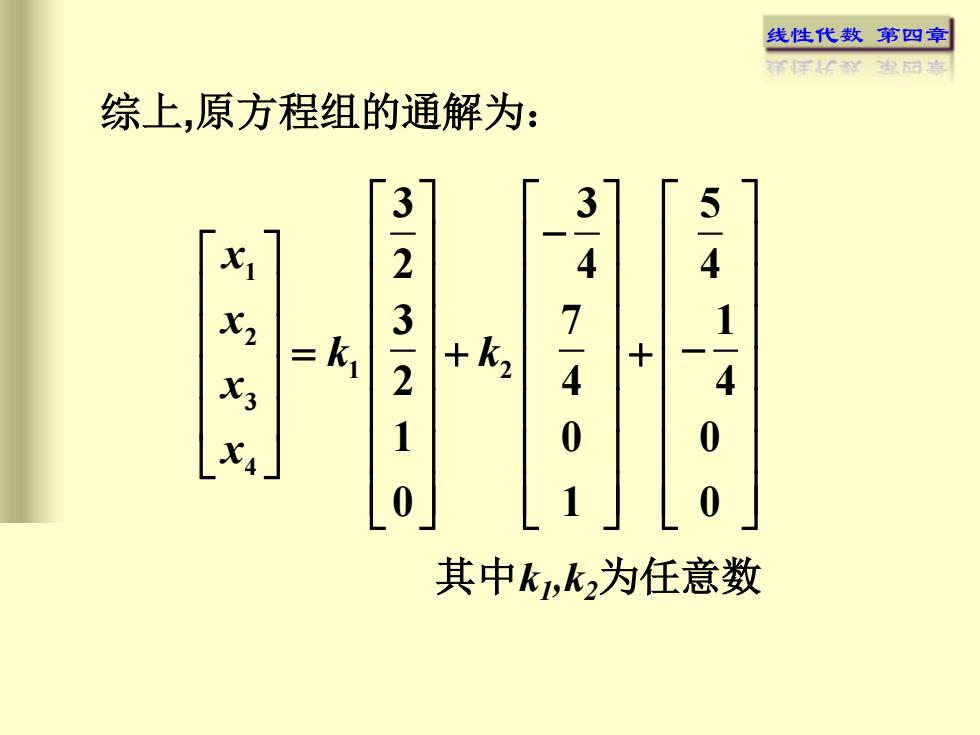
线性代数第四章祥代彩光国堂综上,原方程组的通解为：3-23-2534xxx7k+kz=1410其中kj,k,为任意数

线性代数 第四章 1 2 1 2 3 4 3 3 5 2 4 4 3 7 1 2 4 4 1 0 0 0 1 0 x x k k x x       −                         = + + −                                     综上,原方程组的通解为： 其中k1 ,k2为任意数

线性代数 第四章祥彩光品堂例2求解方程组X -2x, +3x -x4 =1,3x -x, +5x, -3x = 2,2x +X, +2x -2x4 =3.解：对增广矩阵进行初等行变换11r,-3r[13-1-23-1 1-2A=|3 -1 5-12134070-42 1 2 -2 3/r-2r/07

线性代数 第四章 1 2 3 4 1 2 3 4 1 2 3 4 2 3 1, 3 5 3 2, 2 2 2 3. x x x x x x x x x x x x  − + − =   − + − =   + + − = 例2 求解方程组 1 2 3 1 1 3 1 5 3 2 2 1 2 2 3 A   − −   = − −       − 2 1 3 1 3 1 2 3 1 1 ~ 0 5 4 0 1 2 0 5 4 0 1 r r r r − − −     − −   − −     解： 对增广矩阵进行初等行变换

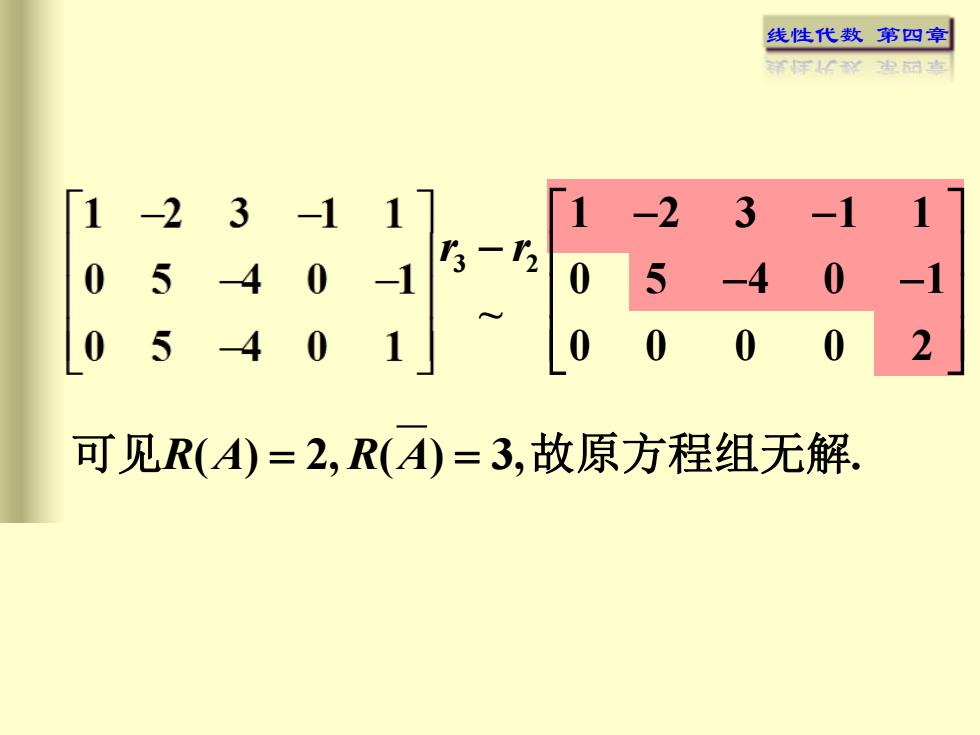
线性代数第四章祥彩光国堂-2311-23-113-125000-4-15-12000005可见R(A)=2,R(A)=3,故原方程组无解

线性代数 第四章 3 2 1 2 3 1 1 0 5 4 0 1 ~ 0 0 0 0 2 r r   − − −   − −       可见R A R A ( ) 2, ( ) 3, . = = 故原方程组无解

线性代数 第四章例3*：求解方程组祥祥花光国--+=0Xi -X, +x -3x =1- - x, -2x, +3x+ =-2解：对增广矩阵进行初等行变换化成行最简形-1r-r-1A=-23-1r3121

线性代数 第四章 1 2 3 4 1 2 3 4 1 2 3 4 0, 3 1, 1 2 3 . 2 x x x x x x x x x x x x  − − + =   − + − =   − − + = −  例3*：求解方程组 1 1 1 1 0 1 1 1 3 1 1 1 1 2 3 2 A   − −   − − =       − − −   2 1 3 1 1 1 1 1 0 0 0 2 4 1 ~ 1 0 0 1 2 2 r r r r   − − −   −     −   − −   解： 对增广矩阵进行初等行变换化成行最简形

线性代数第四章1-21-20-1-10-1-11X22r+r2102-22123+01000可见R(A)= R(A)= 2,故原方程组有解于是得与原方程组同解的方程组：X1 -X,-x4=2'X,=X+X+2即I=2x4X, -2x4X3-2=2

线性代数 第四章 1 2 1 1 1 0 1 2 1 ~ 0 0 1 2 2 0 0 0 0 0 r r   − −   +     −       2 3 2 1 1 1 1 1 0 2 1 ~ 0 0 1 2 2 0 0 0 0 0 r r r    − −     −   +     于是得与原方程组同解的方程组： 1 2 4 3 4 1 , 2 1 2 . 2 x x x x x  − − =    − =  可见R A R A ( ) ( ) 2, . = = 故原方程组有解 1 2 4 3 4 1 , 2 1 2 . 2 x x x x x  = + +    = +  即