
rv() 0%dxdy = [" dy]dxaxJyi(y) axD-f" 2(y,(), y)dy-f" 2(y(y), y)dyQ(x, y)dy - (cur Q(x, y)dyECBEd(yx=yBQ(x, y)dy+ (rcAQ(x, y)dyCBEEACx=V(y)C=f, Q(x,y)dy*x0ap-7dxdy = Φ, P(x, y)dx同理可证ayD
D Q dxdy x 2 1 ( ( ), ) ( ( ), ) d d c c = − Q y y dy Q y y dy ( , ) ( , ) CBE CAE = − Q x y dy Q x y dy ( , ) ( , ) CBE EAC = + Q x y dy Q x y dy ( , ) L = Q x y dy 同理可证 ( , ) L D P dxdy P x y dx y − = y x od 2 x y = ( ) D c CE 1 x y = ( ) B A 2 1 ( ) ( ) d y c y Q dy dx x =

apaQM)dxdy = Φ, Pdx + Qdy两式相加得axayD(2)若区域D由按段光DLD,滑的闭曲线围成.如图将D分成三个既是X-型又是DD,LLY-型的区域D、D,、D,apapaQaQM)dxdy=)dxdyaxayayaxDD,+D2+D3
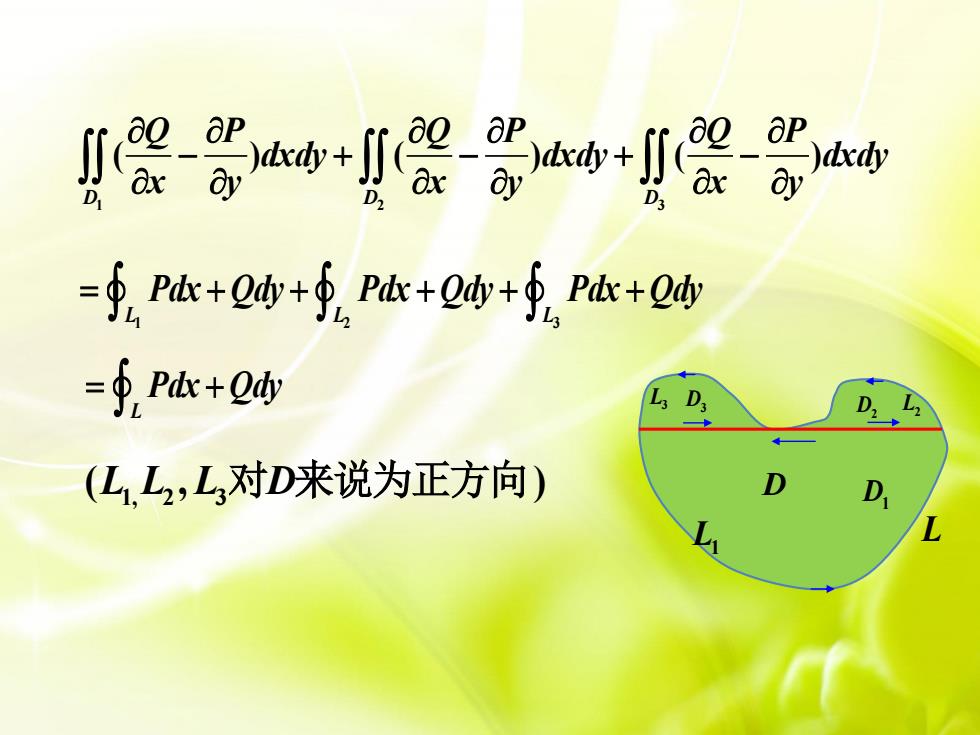
L D (2)若区域D由按段光 滑的闭曲线围成.如图, L1 L3 L2 D1 D2 D3 两式相加得 ( ) L D Q P dxdy Pdx Qdy x y − = + 1 2 3 ( ) ( ) D D D D Q P Q P dxdy dxdy x y x y + + − = − 1 2 3 D X Y D D D − − 将 分成三个既是 型又是 型的区域 、
apapap0QaQaQJsJ)dxdy)dxdy)dxdy ++axaxayayaxayD3D,e Pdx+ Qdy+$, Pdx+Qdy+ Φ, Pdx+QdyJLJLs= $, Pdx + QdyL3DsD2(L,L,L,对D来说为正方向)DDL4
1 2 3 ( ) ( ) ( ) D D D Q P Q P Q P dxdy dxdy dxdy x y x y x y − + − + − L L L 1 2 3 = + + + + + Pdx Qdy Pdx Qdy Pdx Qdy L = + Pdx Qdy 1, 2 3 ( , ) L L L D 对 来说为正方向 L L1 L2 L3 D D1 D2 D3
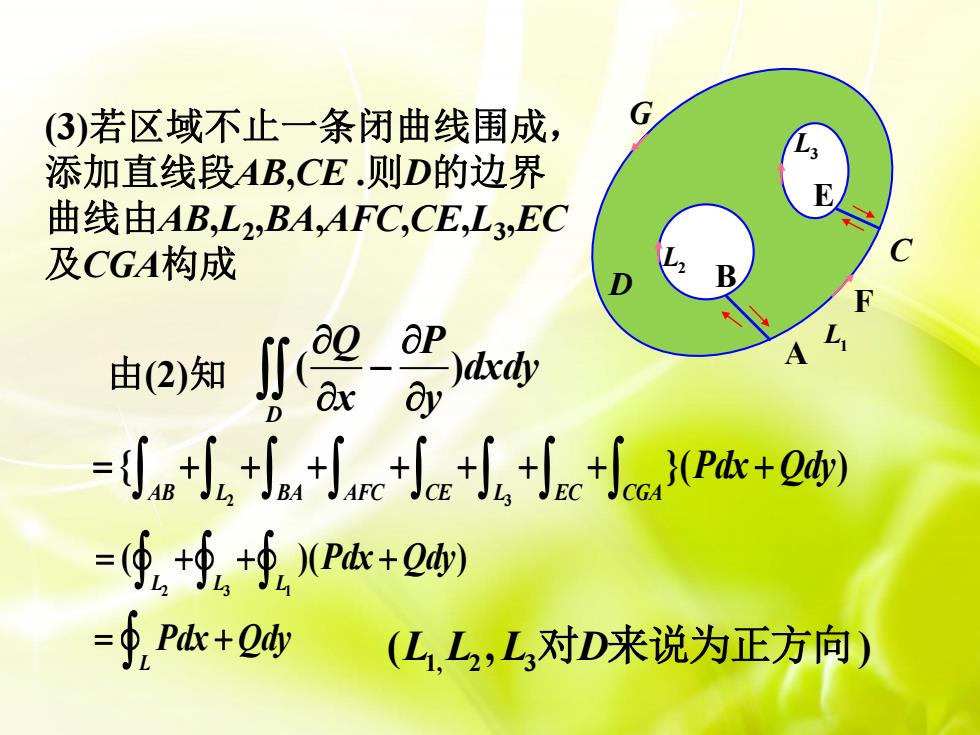
G(3)若区域不止一条闭曲线围成L3添加直线段AB.CE.则D的边界E曲线由AB,L,,BA,AFC,CE,L3,ECc及CGA构成2BDFapLiaQA)dxdy由(2)知axayD=J+J+J+Jarc++J+Je+I(Pdx + Qdy)=(, +9,+, (Pax+ 2d)= d, Pdx +Qdy(L,L2,L,对D来说为正方向)
GD L 3 L 2 F C E L1 A B 由(2) 知 ( ) D Q P dxdy x y − 2 3 { }( ) AB L BA AFC CE L EC CGA = + + + + + + + + Pdx Qdy L = + Pdx Qdy 2 3 1 ( )( ) LLL = + + + Pdx Qdy 1, 2 3 ( , ) L L L D 对 来说为正方向 (3)若区域不止一条闭曲线围成, 添加直线段AB ,CE . 则 D的边界 曲线由AB , L 2 ,BA ,AFC,CE , L 3 ,EC 及CGA构成

apaQJ 4、简单应用)dxdy = Φ, Pdx + QdyaxayD(1).简化曲线积分例1 计算I=Φ,e'dx +(xy3 + xe'-2y)dy,其中L为圆周x2+2=2x的正向解 P=e',Q=xy+xe'-2y山apaQeLy3 +e"ayax02xaqap公.axay由格林公式有 I={[y'dxdy= 0D
解 , y P = e Q xy xe y y 2 3 = + − , y e y P = y y e x Q = + 3 3 y y P x Q = − 由格林公式有 3 d d D I y x y = = 2 . 1 例1 3 d ( 2 )d , y y L I e x xy xe y y = + + − 计算 其中L为圆周 x y 2x 2 2 + = 的正向. O x y 0 (1). 简化曲线积分 4、简单应用 ( ) L D Q P dxdy Pdx Qdy x y − = +