
9.6多元函数微分学的几何应用人民邮电出版社RISSAHITOTRES
9.6 多元函数微分学的几何应用

本讲内容空间曲线的切线与法平面0102空间曲面的切平面与法线
本讲内容 01 空间曲线的切线与法平面 02 空间曲面的切平面与法线
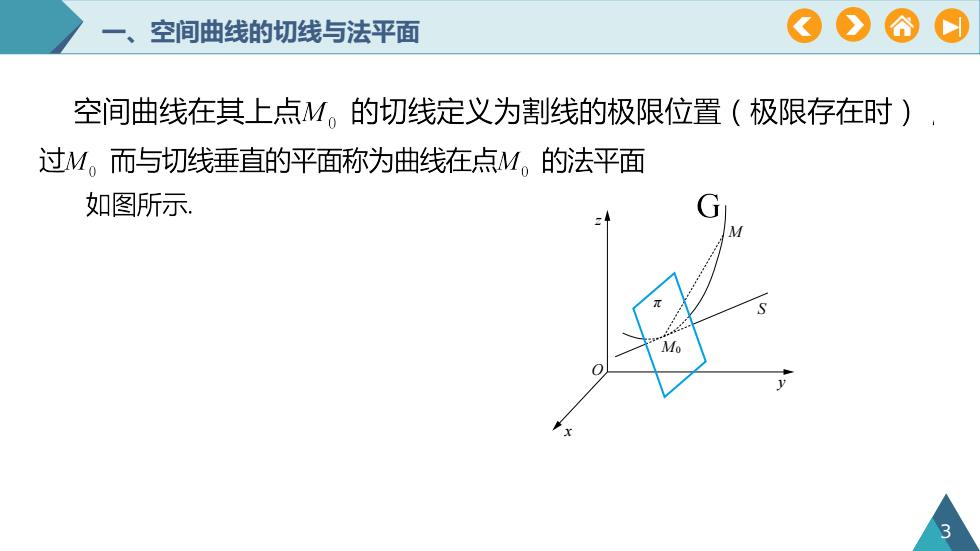
COAO一、空间曲线的切线与法平面空间曲线在其上点M。的切线定义为割线的极限位置(极限存在时)过M。而与切线垂直的平面称为曲线在点M。的法平面如图所示G2Mo
一、空间曲线的切线与法平面 z O x y S M0 M π 3
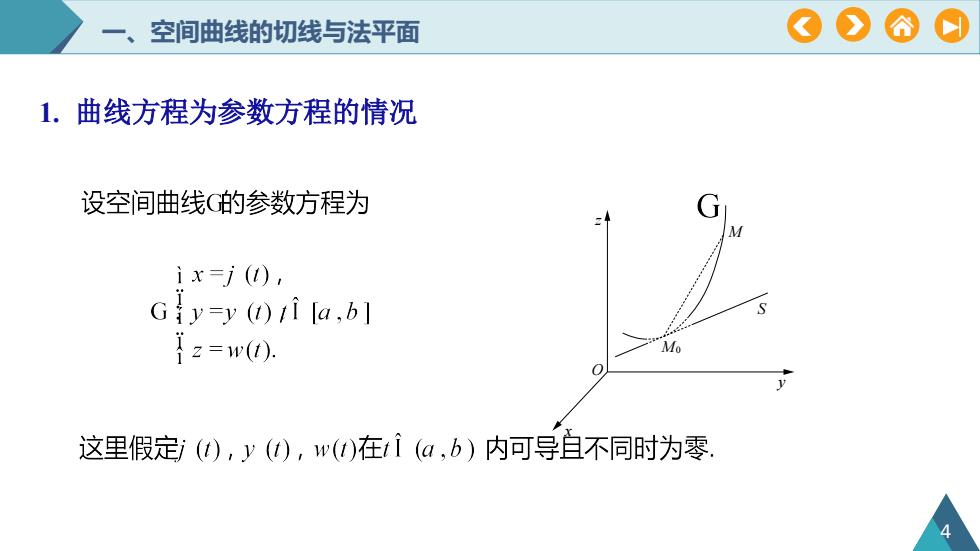
OOA、空间曲线的切线与法平面1.曲线方程为参数方程的情况设空间曲线G的参数方程为GMix=j (l),Giy=y (t) ri [a,b]S1 z = w(0).MoL这里假定j(t),y(U),w(t)在tl(a,b)内可导不同时为零
一、空间曲线的切线与法平面 z O x y S M0 M 4 1. 曲线方程为参数方程的情况

OO#0一、空间曲线的切线与法平面现在要求曲线G上一点M。(x.o,z。)处的切线和法平面方程.这里x。=j (to), o =y (to), zo =w(to), t,i [a,bl且月+月+w眉0.在曲线G上点M(x,y,z的附近取一点M(x+Dx,y+Dy,z。+Dz),对应的参数是t。+Dr(Dr!0),作曲线的割线MM。X-Xo-y-yo-z-zoM其方程为DxDzDy其中Dx=j (t+Dr)- j (to),Dy =y (t+Dt)- y (to),Dz =w (tg+Dr)- w(to)M以D除上式各分母,得JX- XoZ- Zoy-yoDyDzDxDtDtDt
一、空间曲线的切线与法平面 5 z O x y S M0 M