
五、可导与连续的关系 例10.证明f(x)=在x=0连续但不可导 证明:显然fx)=F是基本初等函数,且x=0是fx)定义域内一点, (1)故f(x)在x=0处连续 (2)又Ar≠0时,Ay=f0+A)-f0)_△-0」 △x (a可 所以im y=0, x-0△ 故1mAy不存在,因此)=在x=0不可导 Ax-0Ar 2 y=/x X
例 10.证明 3 fx x x () 0 = 在 = 连续但不可导 证明:显然 3 f ( ) x x = 是基本初等函数,且 x = 0是 f ( ) x 定义域内一点, (1)故 f ( ) x 在 x = 0处连续 (2)又Δ ≠ x 0 时, ( ) 3 2 3 yf xf x (0 ) (0) 0 1 xx x x Δ +Δ − Δ − = == ΔΔ Δ Δ 所以 0 lim x y Δ → x Δ = ∞ Δ ,故 0 limx y Δ → x ΔΔ 不存在,因此 3 fx x x () 0 = = 在 不可导 x y 0 1 3 y = x 五、可导与连续的关系
§2.2函数和积商的求导法则 函数和的 主要 求导法则 函数积的 内 11I 求导法则 函数积的 求导法则的应用 容 求导法则
主 要 内 容 函数和的 求导法则 §2.2 函数和积商的求导法则 函数积的 求导法则 函数积的 求导法则 求 导 法 则 的 应 用
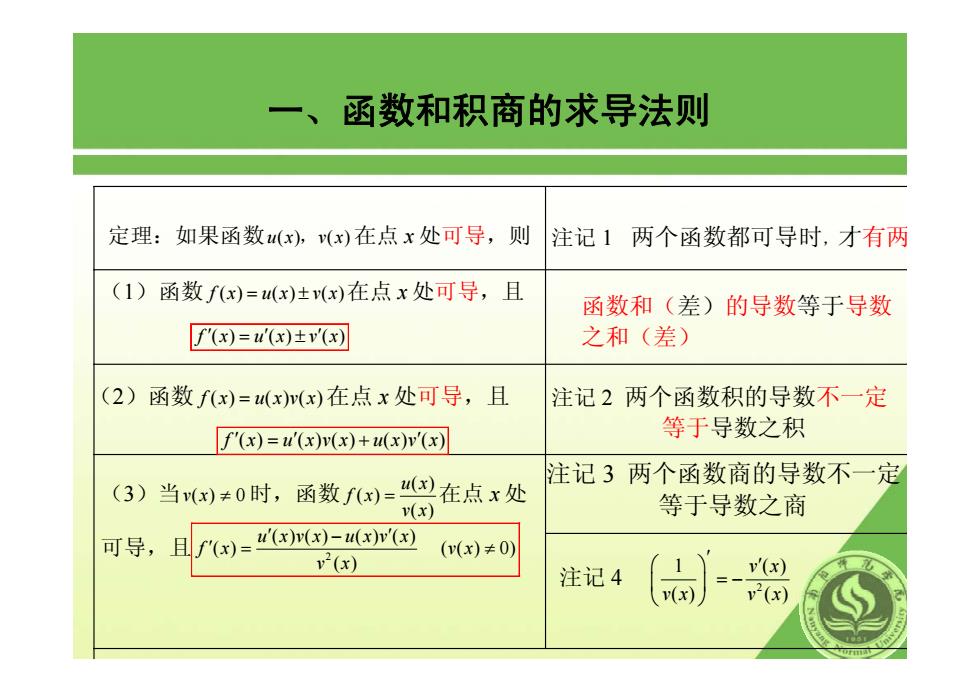
一、函数和积商的求导法则 定理:如果函数ux,x)在点x处可导,则 注记1两个函数都可导时,才有两 (1)函数fx)=(x)士(x)在点x处可导,且 函数和(差)的导数等于导数 f'(x)=u'(x)±v'(x) 之和(差) (2)函数fx)=(x)(x)在点x处可导,且 注记2两个函数积的导数不一定 f'(x)=u(x)r(x)+4(x)v'(x) 等于导数之积 (3)当x)≠0时,函数f=在点x处 注记3两个函数商的导数不一定 v(x) 等于导数之商 可导, 且f'G)=x)-4xP (v(x)≠0) v(x) 注记4 v'(x) v(x) v2(x)
一、函数和积商的求导法则 定理:如果函数ux vx () () , 在点 x 处可导,则 ( 1) 函数 f () () () x ux vx = ± 在点 x 处可导,且 f ′ ′′ () () () x ux vx = ± ( 2)函数 f () ()() x uxvx = 在点 x 处可导,且 f ′′ ′ () ()() () () x u xvx uxv x = + ( 3)当 v(x) ≠ 0 时,函数 ( ) ( ) ( ) u x f x v x = 在点 x 处 可导,且 2 ()() () () ( ) ( ( ) 0) ( ) u xvx uxv x f x vx v x ′ ′ − ′ = ≠ 注记 1 两个函数都可导时,才 有 两 函数和(差)的导数等于导数 之和(差) 注记 2 两个函数积的导数不一定 等于导数之积 注记 3 两个函数商的导数不一定 等于导数之商 注记 4 2 1 () () () v x vx v x ′ ⎛ ⎞ ′ ⎜ ⎟ = − ⎝ ⎠

证明: 如果函数u(x,(x)在点x处可导,函数fx)=(x)+x) 在点x处也可导 设f(x)=u(x)+v(x) 已知函数(x),(x)在点x处可导 0 Ay=fx+△x)-fx)=[x+△x)+x+△x-[x)+x] =[u(x+△x)-(x]+[y(x+△x)-v(x]=△u+△y lim △4='(x) Ar0 lim △ △r-→0△x =(x Ay=fx+A)-f田=w+A" △x △x△x △y lim =lim f(x+△x)-f(x) △u,△v lim Ar-→0△x 4r-0 △x 4r-0 △x △x △u △V lim+lim=u'(x)+v(x) Ar0△xAr→0△x
证明:如果函数ux vx () () , 在点 x 处可导,函数 f () () () x ux vx = + 在点 x 处也可导 已知函数ux vx () () , 在点 x 处可导 0 0 lim ( ) lim ( ) x x u u x x v v x x Δ → Δ → Δ = ′ Δ Δ = ′ Δ 设 f x ux vx () () () = + Δ = +Δ − = +Δ + +Δ − + y f x x f x ux x vx x ux vx ( ) () ( ) ( ) () () [ ] [ ] = +Δ − + +Δ − [ux x ux vx x vx ( ) () ( ) () ][ ] = Δ +Δ u v y fx x fx u v ( ) () x x xx Δ +Δ − Δ Δ = =+ Δ Δ ΔΔ 00 0 0 0 ( ) () lim lim lim = lim lim ( ) ( ) xx x x x y fx x fx u v x x xx u v ux vx x x Δ→ Δ→ Δ→ Δ→ Δ→ Δ +Δ − Δ Δ ⎡ ⎤ = =+ ⎢ ⎥ Δ Δ ΔΔ ⎣ ⎦ Δ Δ + =+ ′ ′ Δ Δ
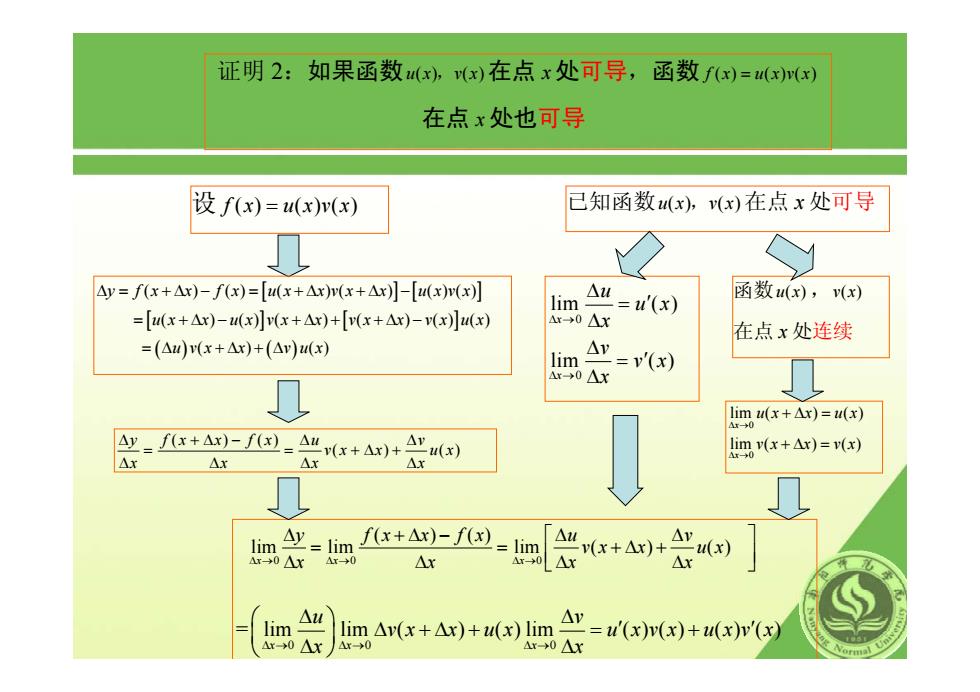
证明2:如果函数,)在点x处可导,函数fx)=()m(x) 在点x处也可导 设f(x)=(x)(x) 已知函数(x),v(x)在点x处可导 △y=f(x+△x)-f(x)=[u(x+△x)(x+△x]-[u(x)vx] △u ='(x) 函数u(x),v(x) lim =[u(x+△r)-(x小x+△x)+[(x+△r)-(x]u(x) △r→0△x 在点x处连续 =(△0y(x+△x)+(△v)u(x) lim △ =v'(x) Ar→0△x 0 mx+A)=)) △y=fx+A)-f☒-A“x+△x)+A Ar") lim(x+Ar)=v(x) △r △x △r △y f(x+Ax)-f(x)=lim △u lim =lim Ar→0Ax △x r-0△x +a+ △u lim lim△v(x+△x)+u(x)lim △x→0△X △r→0 =u(x)v(x)+u(x)v(x) Ax-→0△x
证明 2:如果函数ux vx () () , 在点 x 处可导,函数 f () ()() x uxvx = 在点 x 处也可导 已知函数ux vx () () , 在点 x 处可导 0 0 lim ( ) lim ( ) x x u u x x v v x x Δ → Δ → Δ = ′ Δ Δ = ′ Δ 设 f x uxvx () ()() = ( ) () ( ) ( ) y fx x fx u v vx x ux x xx x Δ +Δ − Δ Δ = = +Δ + ΔΔΔ Δ Δ = +Δ − = +Δ +Δ − y f x x f x ux xvx x uxvx ( ) () ( )( ) ()() [ ] [ ] = +Δ − +Δ + +Δ − [ux x ux vx x vx x vx ux ( ) () ( ) ( ) () () ] [ ] = Δ +Δ + Δ ( uvx x vux ) () ( ) () 00 0 ( ) () lim lim lim ( ) ( ) xx x y fx x fx u v vx x ux Δ→ Δ→ Δ→ x x xx Δ +Δ − Δ Δ ⎡ ⎤ = = +Δ + ⎢ ⎥ Δ Δ ΔΔ ⎣ ⎦ 00 0 = lim lim ( ) ( ) lim ( ) ( ) ( ) ( ) xx x u v vx x ux u xvx uxv x Δ→ Δ→ Δ→ x x ⎛ ⎞ Δ Δ Δ +Δ + = + ′ ′ ⎜ ⎟ ⎝ ⎠ Δ Δ 函数u x( ) ,v x( ) 在点 x 处连续 0 0 lim ( ) ( ) lim ( ) ( ) x x ux x ux vx x vx Δ → Δ → + Δ = +Δ =