
部分初等函数的的求导公式 (1)(C)=0 (2)(sinx)'=cos x. (3)(cos x)'=-sinx. (④ (a")'=a*Ina. ⑤(e)'=e (6)(x“)'=4x“-(为常数)
部分初等函数的的求导公式 4 ( ) ln . x x () a aa ′ = 5 ()x x () e e ′ = ( 1 ) ( ) C 0 ′ = ( 2 ) (sin x )′=cos x . ( 3 ) (cos x )′= -sin x . ( 6 ) 1 ( ) x x μ μ μ μ − ′ = ( 为常数)

四、导数的应用 (1)用导数的定义求极限 例8:求im (x+)0-xw 1→0 h 分析:设=则任+小--+仙-国因 h h g任+w 产=回+的国- >0 h 解:令fx)=x,f"(x)=100x”由导数的定义可知 lim ”=lim+)-f=f=100x h→0 h h→0 h
四、导数的应用 (1)用导数的定义求极限 例 8: 求 ( )100 100 0 limh xh x → h + − 分析: 设 100 f () , x x = 则 ( )100 100 xh x f ( ) () x h fx h h + − + − = 因此 ( )100 100 0 0 ( ) () lim lim ( ) h h xh x fx h fx f x → → h h + − + − = = ′ 解:令 100 fx x () , = 99 fx x ′( ) 100 = 由导数的定义可知 ( )100 100 99 0 0 ( ) () lim lim ( ) 100 h h xh x fx h fx f x x → → h h + − + − = == ′

四、导数的应用 (2)求曲线的切线及法线 例9 求在点32 的切线和法线方程 解: 1)由于y=(月=ヅ- (2)由导数的几何意义知,y=在点传2的切线的斜来人=y=-4 (3)所求的切线方程为y-2=-4x-)即4x+y-4=0 (4)所求的法线方程为”-2=x-之即2x-8y+15=0
四、导数的应用 (2)求曲线的切线及法线 例 9 求 1 y x = 在点 1 , 2 2⎛ ⎞ ⎜ ⎟ ⎝ ⎠的切线和法线方程 解:(1)由于 ( ) 1 1 2 y xx x − − ′ ⎛ ⎞ ′ ′ = = =− ⎜ ⎟ ⎝ ⎠ (2)由导数的几何意义知, 1 y x = 在点 1 , 2 2⎛ ⎞ ⎜ ⎟ ⎝ ⎠的切线的斜率 12 4 x k y = = ′ = − (3)所求的切线方程为 1 2 4( ) 2 y x − =− − 即4 40 x y + − = (4)所求的法线方程为 1 1 2( ) 4 2 y x − = − 即2 8 15 0 x y − + =
探究可导与连续的关系 若函数y=fx)在点xo处可导 函数y=fx)在点xo处连续 lim △y=f'(x) 4x→0△x imAy=0 极限与无穷小的关系 &=f)+ata→0 limAy=lim(f(x)Ax)+lim(cAx) △x-0 △y=f'(xo)△x+a△x(a→0) iAy=lim[f(o)Ax+aAx]
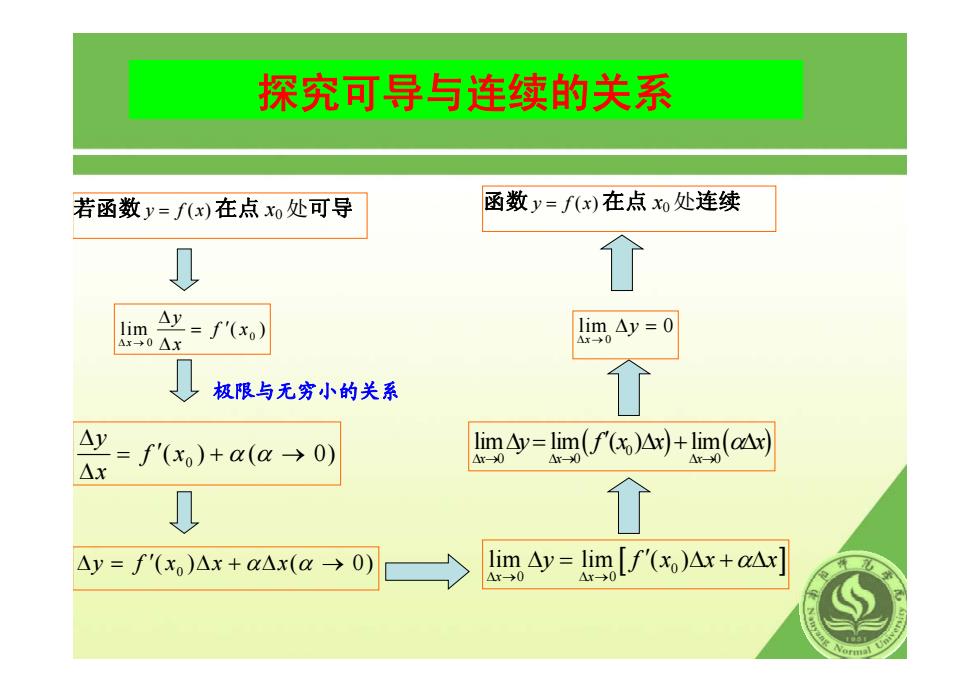
探究可导与连续的关系 若函数 y fx = ( ) 在点 x 0 处可导 0 0 lim ( ) x y f x Δ → x Δ = ′ Δ 极限与无穷小的关系 0 ( ) ( 0) y f x x α α Δ = +→ ′ Δ 0 Δ= Δ+ Δ → y fx x x ′( ) ( 0) α α [ 0 ] 0 0 lim lim ( ) x x y f xx x α Δ→ Δ→ Δ = Δ+ Δ ′ ( ) ( ) 0 00 0 lim lim ( ) lim xx x y f xx x α Δ→ Δ→ Δ→ Δ = Δ+ Δ ′ 0 lim 0 x y Δ → Δ = 函数 y fx = ( ) 在点 x 0 处连续

五、可导与连续的关系 定理2:若函数y=fx) 注记7:在点x0处连续的函数在点x处不一定可导 在点x和处可导则 即连续是可导的必要条件,但不是充分条件. 函数y=f(x)在 点x0处连 注记8:若函数y=f(x)在点x处不连续,则函数 续 y=f(x)在点xo处不可导
五、可导与连续的关系 定理 2:若函数 y f = ( ) x 在点 x 0 处可导则 函数 y f = ( ) x 在 点 x 0 处 连 续 注记 7: 在点 x 0 处连续的函数在点 x 0 处不一定可导 即连续是可导的必要条件,但不是充分条件. 注记 8:若函数 y fx = ( )在点 x 0处不连续,则函数 y fx = ( )在点 x 0处不可导