
三、导函数 注记7:用定义求导数f(x)的一般步骤: 第一步:求△y=fx+△x)-fx方 第二步:求Ay-x+Aw)-田 Ax △x 第三步:求极限y=lim Ay A-0△x 例4.求函数x)上C(C为常数)的导数. 解: (1)显然△y=f(x+△x)-fx)=C-C=0 (2) 所以4业=0 Ax (3) y=0 故y=
例 4.求函数 f(x)=C(C 为常数)的导数. 解:(1)显然Δ = +Δ − = − = y fx x fx C C ( ) () 0 (2)所以 0 y x Δ = Δ (3)故 0 lim 0 x y y Δ → x Δ ′ = = Δ 注记 7:用定义求导数 f ′( ) x 的一般步骤: 第一步:求Δy fx x fx = +Δ − ( ) ( ); 第二步:求 ( ) (); y f x x f x x x Δ +Δ − = Δ Δ 第三步:求极限 0 lim . x y y Δ → x Δ ′ = Δ 三、导函数

三、导函数 例5.设函数fx)=x”(n为正整数)求f'(x) 分析(1)(x+△x)=x”+Cx-(△x)+Cx-2(△x)2++Cx-(△x)+…+(△x)” △y=[(x+△x)”-x"]=[x-△x+Cx-2(△x)2+…+(△x)] (2)是=m+ca)++a (3)limC%x"-2(△x)=…=lim(△x)”-1=0 A30 所以 (x")'=lim y=1 Ax-0
例 5.设函数 f(x)=x n (n 为正整数) 求 f x ′( ) 分析 (1)( ) () () () () 2 11 2 2 n k n n n n k nk nn n x x x Cx x Cx x Cx x x −− − +Δ = + Δ + Δ + + Δ + + Δ " " (2) 1 22 1 () () nn n n y nx C x x x x Δ −− − = + Δ + +Δ Δ " (3) 22 1 0 0 lim ( ) lim ( ) 0 n n n x x Cx x x − − Δ→ Δ→ Δ == Δ = " 1 22 2 [( ) ] [ ( ) ( ) ] nn n n n n y x x x nx x C x x x − − Δ = +Δ − = Δ + Δ + + Δ " 所以 1 0 ( ) lim n n x y x nx x − Δ → Δ ′ = = Δ 三、导函数

三、导函数 一般地: (x“y=x-(为常数) 2V(x>0) xly=(←1x1=- (x≠0)
一般地: 1 ( ) x x μ μ μ μ − ′ = ( 为常数) 1 1 2 1 1 ( ) ( 0) 2 2 xx x x − ′ = = > ( ) 1 ′ − x 1 1 ( 1) − − = − x 2 1 ( 0) x x = − ≠ 三、导函数
三、导函数 例6.证明 sinx) sina-sin B=2cosBsina-B 2 2 证明:由三角公式可得4y=n+A-n=2oas(+加宁 sin Ar 所以 2 +△x cosx+ 2 sin Ar 故(sinx)'=lim 义= 2.lim cos x+ lim Ar-0 △r 4r-0 2 sint.lim cos(+)=cosx 0 I 1+0 同理可证 cosx) =-sinx
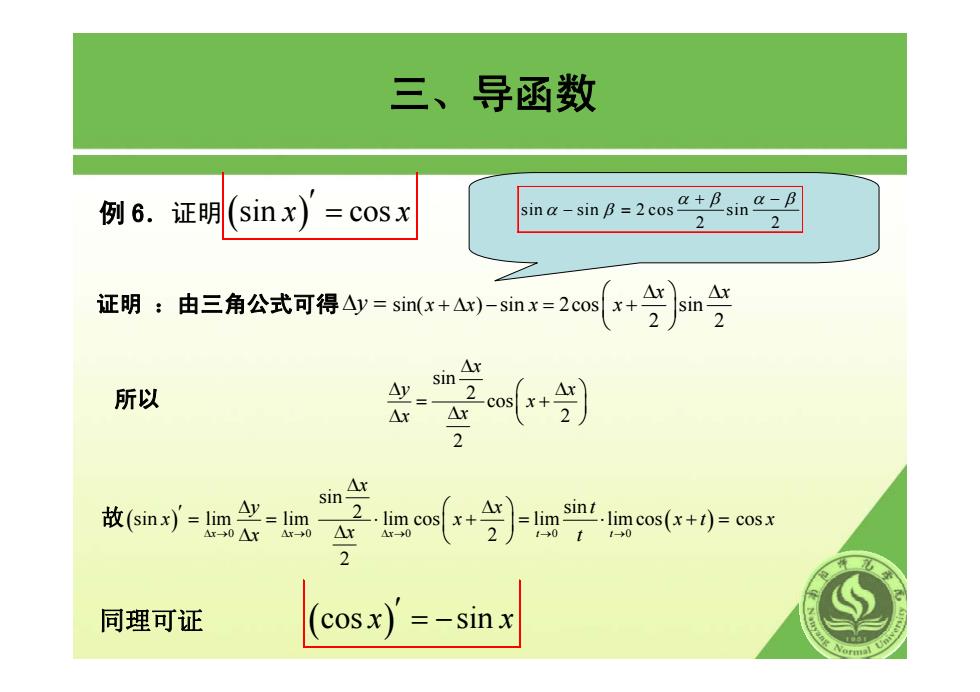
例 6.证明( ) sin cos x x ′ = 证明 :由三角公式可得Δy = sin( ) sin 2cos sin 2 2 x x xx x x ⎛ ⎞ Δ Δ +Δ − = + ⎜ ⎟ ⎝ ⎠ 所以 sin 2 cos 2 2 x y x x x x Δ Δ ⎛ ⎞ Δ = + ⎜ ⎟ Δ Δ ⎝ ⎠ 故( ) 0 0 sin lim lim x x y x Δ→ Δ→ x ′ Δ = = Δ ( ) 0 00 sin sin 2 lim cos lim lim cos 2 2 x tt x x t x xt x t Δ→ → → Δ ⎛ ⎞ Δ ⋅ ⎜ ⎟ + = ⋅ += Δ ⎝ ⎠ cos x 同理可证 sin sin 2 cos sin 2 2 α β αβ α β + − − = ( ) cos sin x x ′ = − 三、导函数

例7.求函数x)=a'(a>0,a≠1)的导数 分析(1)△y=a+r-a=a'(aAr-1) 由于N=enw→ar=eaa=ra→△y=a'(eArina-l) (2)y-e-D-ae- Ax △x Ax 由于当B→0时,e2-1~B.当△x0时,△xlna→0,从而eaa-1-△xlna (3)lim Av=a'lim -→0△x etna1=alim A+0△x △xlna=alna Ar0△x (a")'=a"Ina
例 7.求函数 f(x)= ( 0, 1) x aa a > ≠ 的导数. 分析 (1) ( 1) xx x x x y a a aa +Δ Δ Δ= − = − 由于 ln ln ln x N x a xa Ne a e e Δ Δ Δ = ⇒= = ⇒ ln ( 1) x xa y aeΔ Δ == − (2) ln ln ( 1) ( 1) x xa xa y ae e x a xx x Δ Δ Δ− − = = ΔΔ Δ 由于当β → 0时,e 1 β − ∼ β .当Δx → 0时,Δ → x a ln 0,从而 ln 1 ln x a e xa Δ − Δ ∼ (3) ln 00 0 1 ln lim lim lim ln x a x xx xx x y e xa a a aa xx x Δ Δ→ Δ→ Δ→ Δ −Δ = == ΔΔ Δ ( ) ln x x a aa ′ =