《线性代数》课程教学课件（PPT讲稿，A）5-4 实对称矩阵的相似对角形

线性代数第五车由引理5.4.2(不同特征值的特征向量正交)知对应于不同特征值的特征向量正交，所以这n个单位特征向量两两正交以它们为列向量构成正交矩阵P，有：P-1AP= P-PA = A其中对角矩阵Λ的对角元素含r个，,r个a,恰是A的n个特征值

线性代数 第五章 由引理5.4.2(不同特征值的特征向量正交)知对应 于不同特征值的特征向量正交，所以这n个单位特 征向量两两正交. =  =  − − P AP P P 1 1 1 1 , , , . s s r r A n 其中对角矩阵的对角元素含 个  个 恰 是 的 个特征值 以它们为列向量构成正交矩阵P，有：

线性代数第五章二、实对称矩阵对角化的方法根据上述结论，利用正交矩阵将对称矩阵化为对角矩阵，其具体步骤为：1.求A的特征值2.由(A-2,E)x =0,求出A的特征向量;3.将特征向量正交化：4.将特征向量单位化5.以特征向量为列向量写出正交矩阵

线性代数 第五章 根据上述结论，利用正交矩阵将对称矩阵化 为对角矩阵，其具体步骤为： 3.将特征向量正交化; 4.将特征向量单位化. 2. ( ) 0, ; 由 A E x A − = i 求出 的特征向量 二、实对称矩阵对角化的方法 5.以特征向量为列向量写出正交矩阵. 1.求A的特征值

线性代数 第五章0例1 设A=330求正交矩阵P，使P-1AP为对角形矩阵解(1)第一步 求A的特征值004-2= (2-2)(4- 2)203-元1A-2E=013-2得特征值 = 2,2 = = 4

线性代数 第五章     − − − − = 0 1 3 0 3 1 4 0 0 A E 2 = − − (2 )(4 ) ,   2, 4. 得特征值 1 = 2 = 3 = 1 4 0 0 1 0 3 1 0 1 3 . A P P AP −     =       例 设 ， 求正交矩阵 ，使 为对角形矩阵 解 (1)第一步 求A的特征值

线性代数 第五章(2)第二步由(A-α,E)x=0,求特征值a,对应的特征向量0对 , =2,由(A-2E)x =0,得基础解系, = 1-1对 , = , = 4,由(A-4E)x = 0,得基础解系075,与恰好正交52 = 0 53 =1LO工所以，52，5两两正交

线性代数 第五章 (2) 0, 第二步 由( A E x − =   i i ) 求特征值 对应的特征向量 1 1 0 2, ( 2 ) 0, 1 1   A E x     = − = =       − 对 由 得基础解系 2 3 2 3 4, ( 4 ) 0, 1 0 0 1 , . 0 1   A E x   = = − =         = =             对 由 得基础解系 ,  2与 3恰好正交 , , . 所以 1  2  3两两正交

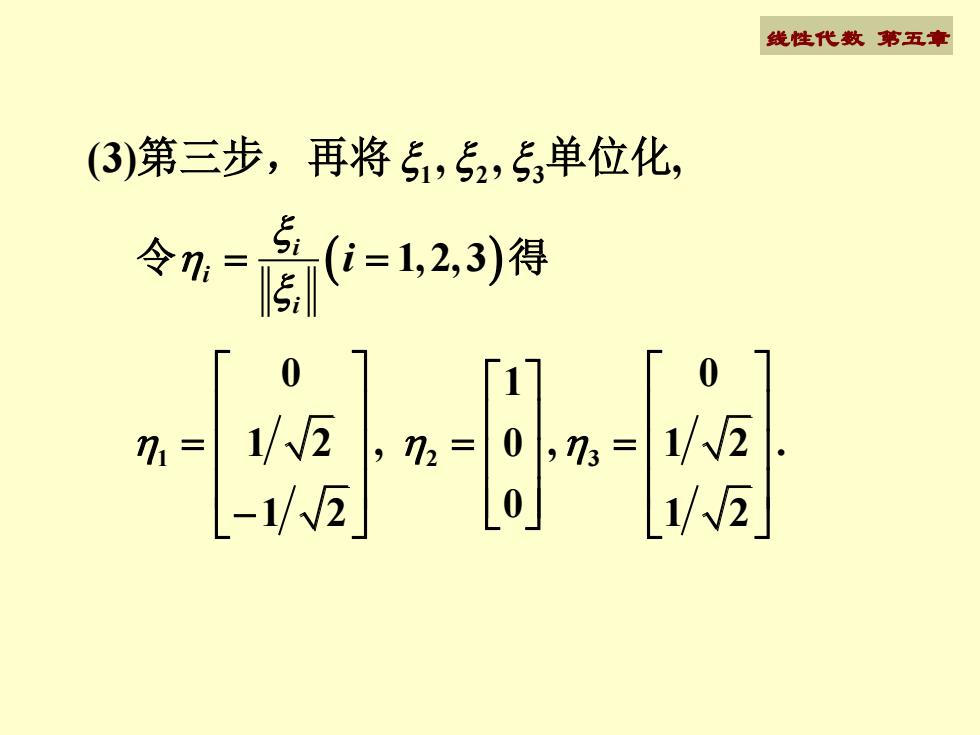
线性代数 第五章(3)第三步，再将51,52,5,单位化5i(i=1,2,3)得令ni15;01/V21/ V22 , n2 =0 |, n3 =ni =1LO[1/ ~2[-1/ ~V2

线性代数 第五章 1 2 3 (3) , , , 第三步，再将    单位化 1 2 3 0 0 1 1 2 0 1 2 , , . 1 2 1 2 0                = = =             −       ( 1,2,3) i i i i    令 = = 得