《线性代数》课程教学课件（PPT讲稿，A）§2.4 矩阵的秩

线性代数 第二章新尔我桃川科定理2.4.3矩阵的行秩等于列秩证：由于mXn矩阵A总可以经过有限次初等变换化为标准形第r行0=101第r列mxn

线性代数 第二章 定理2.4.3 矩阵的行秩等于列秩. 证：由于m×n矩阵A总可以经过有限次初等变换化 为标准形 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 r m n I r           =          第 列 第 行

线性代数 第二章教前尔桃川科而矩阵I的行秩和列秩都等于r，根据定理2.4.1及定理2.4.2的推论知，对A进行初等行变换和初等列变换，它的行秩和列秩都不改变，所以A的行秩和列秩都应等于r，即A的行秩等于列秩定义2.4.2矩阵A的行秩和列秩，统称为矩阵A的秩，记为R(A).对于m×n矩阵A，显然R(A)满足条件：(1) 0 ≤ R(A)≤min(m,n); (2) R(A') = R(A)若A为n阶方阵，且R(A)=n，则称A为满秩矩阵推论 若矩阵A～ B，则R(A)= R(B)

线性代数 第二章 而矩阵I的行秩和列秩都等于r，根据定理2.4.1及定理2.4.2的 推论知，对A进行初等行变换和初等列变换，它的行秩和列秩都 不改变，所以A的行秩和列秩都应等于r，即A的行秩等于列秩. 定义2.4.2 矩阵A的行秩和列秩，统称为矩阵A的秩，记为R(A). ( ) 0 ( ) min{ , }; (2) ( ) ( ) ( ) . T m n A R A R A m n R A R A A n R A n A    = = 对于 矩阵 ，显然 满足条件： (1) 若 为 阶方阵，且 ，则称 为满秩矩阵 推论 ~ ( ) ( ). 若矩阵A B R A R B ，则 =

线性代数 第二章矩阵秩的求法我尔我轮川复习：行阶梯形矩阵1-2021-13例如:A=B =300-3-1特点：(1)可划出一条阶梯线，线的下方全为零；20(2)每个台阶只有一行，台阶0003数即是非零行的行数，阶梯线的竖线后面的第一个元素00007为非零元，即非零行的第一个非零元

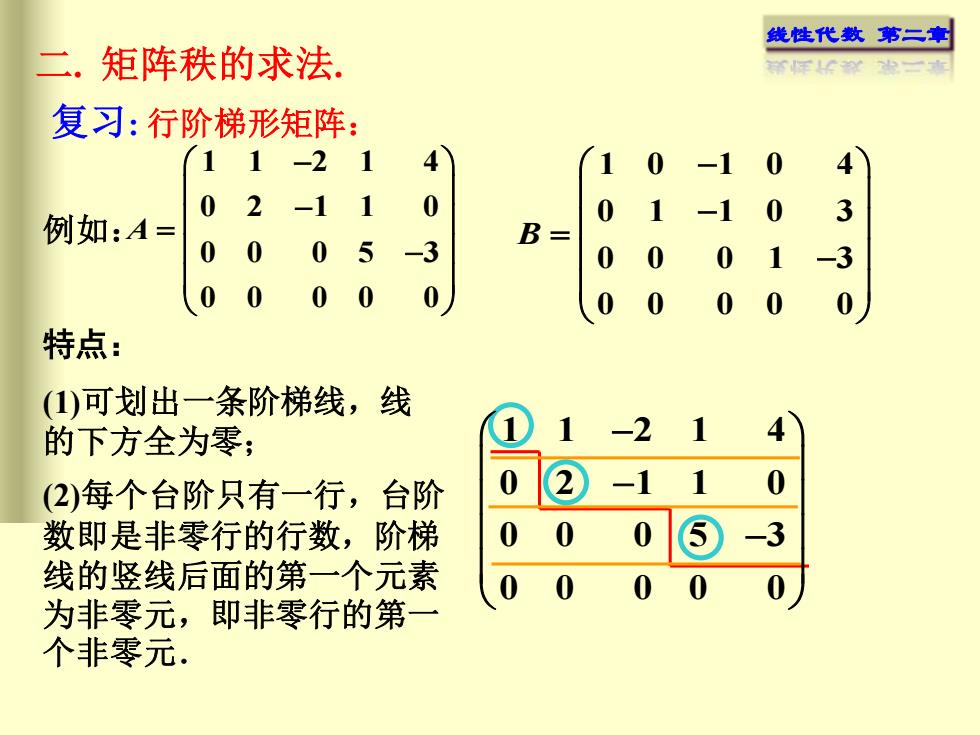
线性代数 第二章 二. 矩阵秩的求法. 复习: 行阶梯形矩阵： 1 0 1 0 4 0 1 1 0 3 0 0 0 1 3 0 0 0 0 0 B   −   − =     −     例如： 1 1 2 1 4 0 2 1 1 0 0 0 0 5 3 0 0 0 0 0 A   −   − =     −     特点： (1)可划出一条阶梯线，线 的下方全为零； (2)每个台阶只有一行，台阶 数即是非零行的行数，阶梯 线的竖线后面的第一个元素 为非零元，即非零行的第一 个非零元． 1 1 2 1 4 0 2 1 1 0 0 0 0 5 3 0 0 0 0 0   −   −     −    