《线性代数》课程教学课件（PPT讲稿，A）§2.4 矩阵的秩

线性代数 第二章 1 2 , , 设m n A  矩阵 的行向量组   ， m ，且 1 1 ~ i j i j i r kr j j m m k A B          +                   +     = =                            

线性代数 第二章 1 1 ( ) i i j j m m k k         = = + − = 由 可知，矩阵A的行向量组可由B的行向量组线性表示. 显然，矩阵B的行向量组可由A的行向量组线性 表示.所以，矩阵A、B的行向量组等价.从而矩阵A、 B的行向量组的秩相同

线性代数 第二章张二本定理2.4.1亦可作为初等变换不改变线性方程组中独立方程的个数的理论依据定理2.4.2初等行(列)变换不改变矩阵列(行)向量间的线性关系.03例3设矩阵A=其列向量-1526042αr,αz,αg,α,间有线性关系：α, =α, +2α,-αg,矩阵矩阵A经过有限次初等行变换得到验证B的列向量β,βz,β3,β,间也有线性关系β =β,+2βz -β3

线性代数 第二章 定理2.4.1亦可作为初等变换不改变线性方程组中 独立方程的个数的理论依据 定理2.4.2 初等行(列)变换不改变矩阵列(行)向量间的 线性关系. 1 2 3 4 4 1 2 3 1 2 3 4 4 1 2 3 1 1 3 0 3 0 2 1 5 6 0 2 4 , , , 2 . , 2 A B A B                     = −       = + − = + − 例 设矩阵 其列向量 间有线性关系： ， 矩阵 由矩阵 经过有限次初等行变换得到 验证 的列向量 间也有线性关系

线性代数 第二章师乐光二解：对矩阵A作初等行变换如下：0013+3r2r3-6ri50252419-1900-164-603Xr-3r31152+r3000

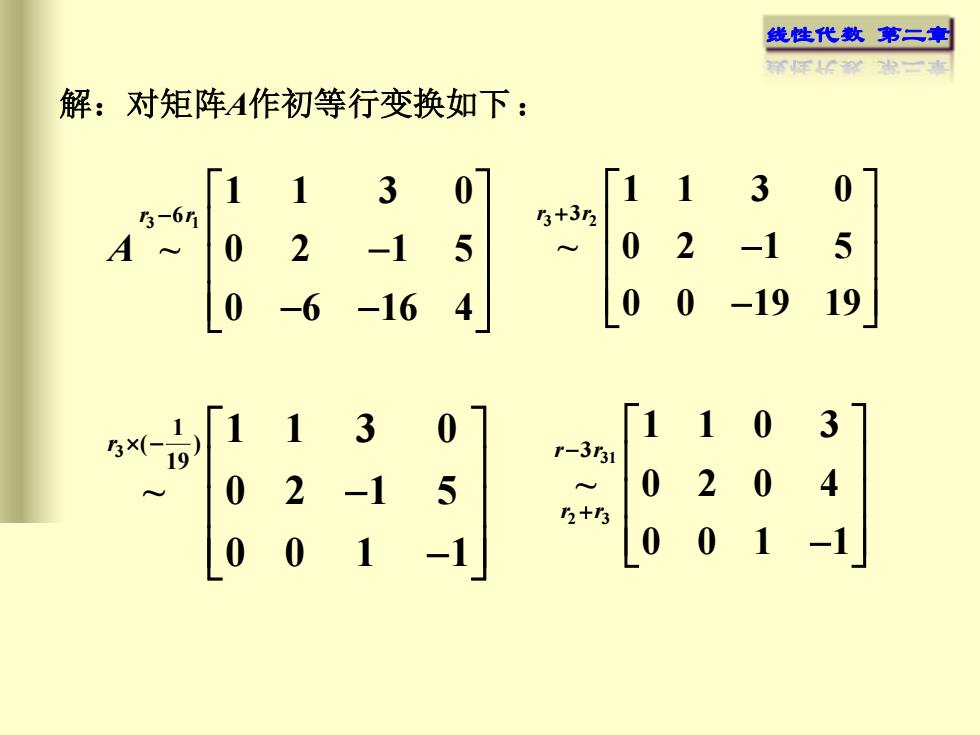
线性代数 第二章 解：对矩阵A作初等行变换如下： 3 1 6 1 1 3 0 ~ 0 2 1 5 0 6 16 4 r r A −     −       − − 3 2 3 1 1 3 0 ~ 0 2 1 5 0 0 19 19 r r +     −       − 3 1 ( ) 19 1 1 3 0 ~ 0 2 1 5 0 0 1 1 r  −     −       − 31 2 3 3 1 1 0 3 ~ 0 2 0 4 0 0 1 1 r r r r − +           −

线性代数 第二章教南乐装城川料013ri-r220=B12容易看出，B的列向量β,β,,β,β间也有线性关系β=β,+2β,-β3实际上，如果把以上每作一次初等行变换所得到的矩阵叫做B的话,B的列向量间同样存在上述线性关系推论初等行(列)变换不改变矩阵的列(行)秩

线性代数 第二章 2 1 2 1 1 0 3 ~ 0 1 0 2 0 0 1 1 r            − 1 2 1 0 0 1 ~ 0 1 0 2 0 0 1 1 r r B −     =       − 1 2 3 4 4 1 2 3 , 2 . B         = + − 容易看出， 的列向量 间也有 线性关系 实际上，如果把以上每作一次初等行变换所得到的 矩阵叫做B的话,B的列向量间同样存在上述线性关系. 推论 初等行(列)变换不改变矩阵的列(行)秩