
(1)分割T =t,<ti <t,<...<tn-1 <th =TAt, = t; -ti-1(2)近似4S, ~v(t,)At,i =1,2,."",nnZ(3)作和则S~v(t,)At;i-1(4)取极限a = max{At,,At,,...,At.]"W路程的精确值S=limV(T)At1-0i=l
(1)分割 1 0 1 2 1 T2 T t t t t t = n− n = i = i − i−1 t t t ( ) 1,2, , (2)近似 S v t i n i i i = 1 ( ) n i i i S v t = 则 (4)取极限 max{ , , , } 1 2 n = t t t 0 1 lim ( ) n i i i S v t → = 路程的精确值 = (3)作和

二、定积分的定义定义设函数f(x)在[a,b]上有界,在[a,b]中任意插入若干个分点a=x<x <x,<.<xn-<x,=b把区间[a,b]分成n个小区间[x;-1,x,](i =1,2,…,n),各个小区间的长度为Axr,=x,-x,-(i=1,2,),在每个小区间上任取一点,(x-≤,≤x,),作乘积f(,)Ar(i= 1,2,),并作和S = Zf(5,)Ax,=记a=max[Ax,,Ax,,,Ax,,如果不论对[a,b]怎样的
定义 0 1 2 1 1 1 1 1 ( ) [ , ] , [ , ] [ , ] [ , ]( 1,2, , ), ( 1,2, ), ( ), ( ) ( 1,2, ), ( ) , max{ n n i i i i i i i i i i i n i i i f x a b a b a x x x x x b a b n x x i n x x x i x x f x i S f x x − − − − = = = = = − = = = = 设函数 在 上有界 在 中任意插入 若干个分点 把区间 成 个小区间 各个小区间的长度为 在每 个小区间上任取一点 作乘积 并作和 记 1 2 , , , }, [ , ] n x x a b 如果不论对 怎样的 二、定积分的定义
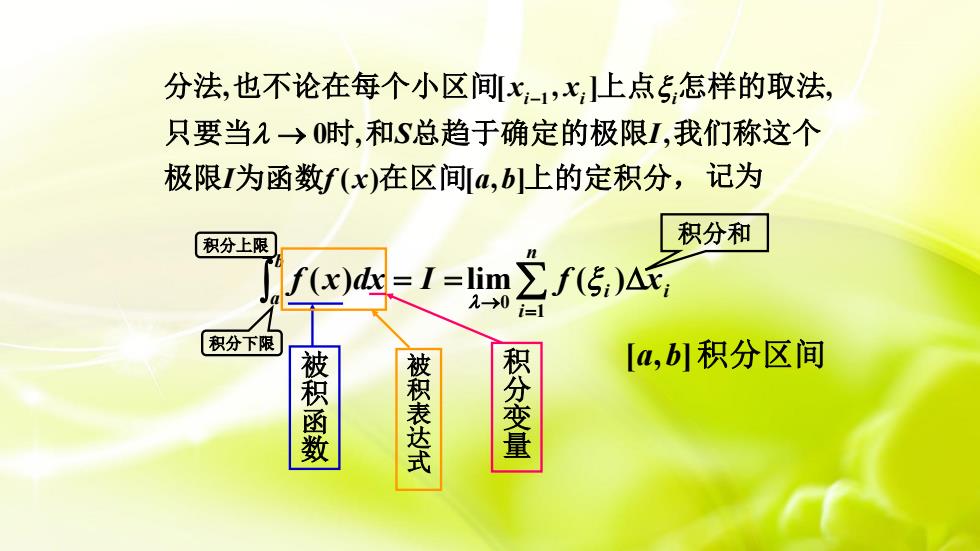
分法,也不论在每个小区间[x-1,x,]上点5,怎样的取法只要当入→0时,和S总趋于确定的极限I,我们称这个极限I为函数f(x)在区间[a,b]上的定积分,记为积分和积分上限f(x)dx= I =limf(5.)Ar2-0积分下限[a,b]积分区间积分变量被积函数被积表达式
= = ba f (x)dx I i i ni f x = → lim ( ) 1 0 被积函数 被积表达式 积分变量 [ , ] a b 积分区间 记为 积分上限 积分下限 积分和 1 , [ , ] , 0 , , ( ) [ , ] i i i x x S I I f x a b − → 分法 也不论在每个小区间 上点 怎样的取法 只要当 时 和 总趋于确定的极限 我们称这个 极限 为函数 在区间 上的定积分,

n['f(x) dx=lim(5)Axa-0定积分实质上就是无穷多个无穷小量的和,它体现了一种无限细分、无限求和的思想。化整为零积零为整
定积分实质上就是无穷多个无穷小量 的和,它体现了一种无限细分、无限求 和的思想。 化整为零 积零为整 ( ) ( ) 0 1 → = = lim n b i i a i f x dx f x
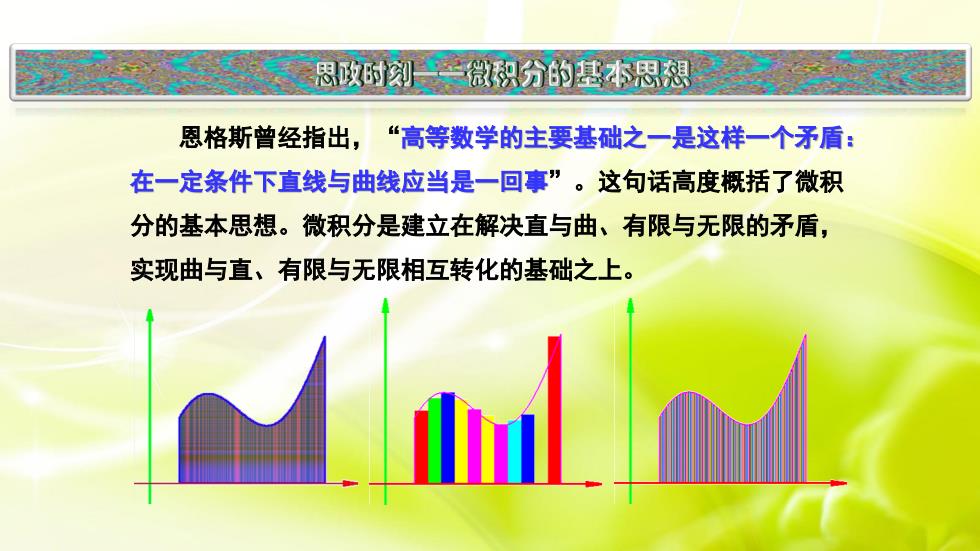
思政时刻微积分的基本思想恩格斯曾经指出,“高等数学的主要基础之一是这样一个矛盾:在一定条件下直线与曲线应当是一回事”。这句话高度概括了微积分的基本思想。微积分是建立在解决直与曲、有限与无限的矛盾实现曲与直、有限与无限相互转化的基础之上
恩格斯曾经指出,“高等数学的主要基础之一是这样一个矛盾: 在一定条件下直线与曲线应当是一回事”。这句话高度概括了微积 分的基本思想。微积分是建立在解决直与曲、有限与无限的矛盾, 实现曲与直、有限与无限相互转化的基础之上