定积分问题举例一实例1(求曲边梯形的面积)Vy=f(x)曲边梯形由连续曲线y= f(x)(f(x)≥0)A=?x轴与两条直线x=a、olabx=b所围成
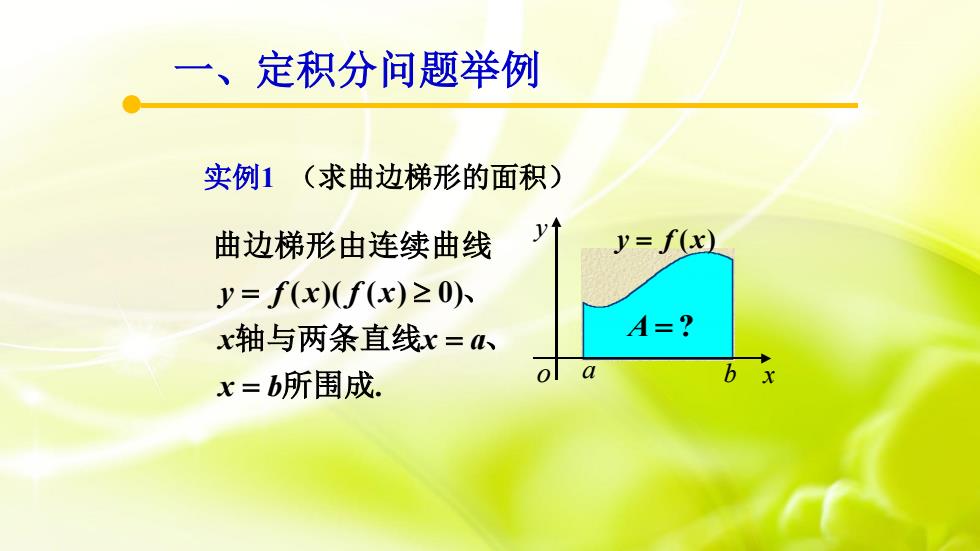
a b x y o A = ? 实例1 (求曲边梯形的面积) y = f (x) 一、定积分问题举例 ( )( ( ) 0) . y f x f x x x a x b = = = 曲边梯形由连续曲线 、 轴与两条直线 、 所围成
以直代曲用矩形面积近似取代曲边梯形面积ba0h0X(四个小矩形)(九个小矩形)显然,小矩形越多,矩形总面积越接近曲边梯形面积
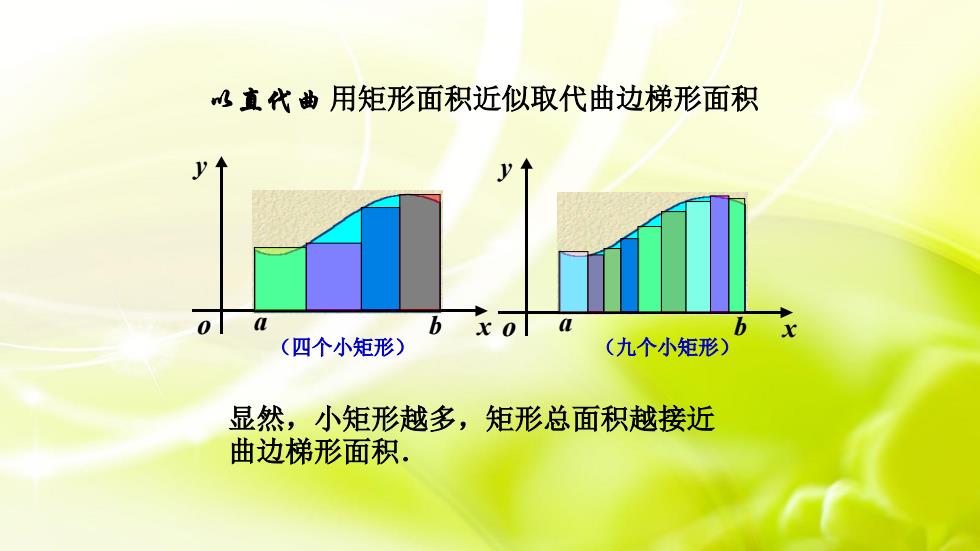
a b x y a b x o y o 以直代曲 用矩形面积近似取代曲边梯形面积 显然,小矩形越多,矩形总面积越接近 曲边梯形面积. (四个小矩形) (九个小矩形)
(1.分割)曲边梯形如图所示,在区间[a,b内任意插入若干个分点a=x<x<x,<…<xn-<x,=b把区间[a,b]分成nJ个小区间[xi-1,x;],长度为Axr;Ax, = X, -Xi-1 olaxXi- X-bi=1,2,..,n;这样,把曲边梯形分割为n个窄曲边梯形;
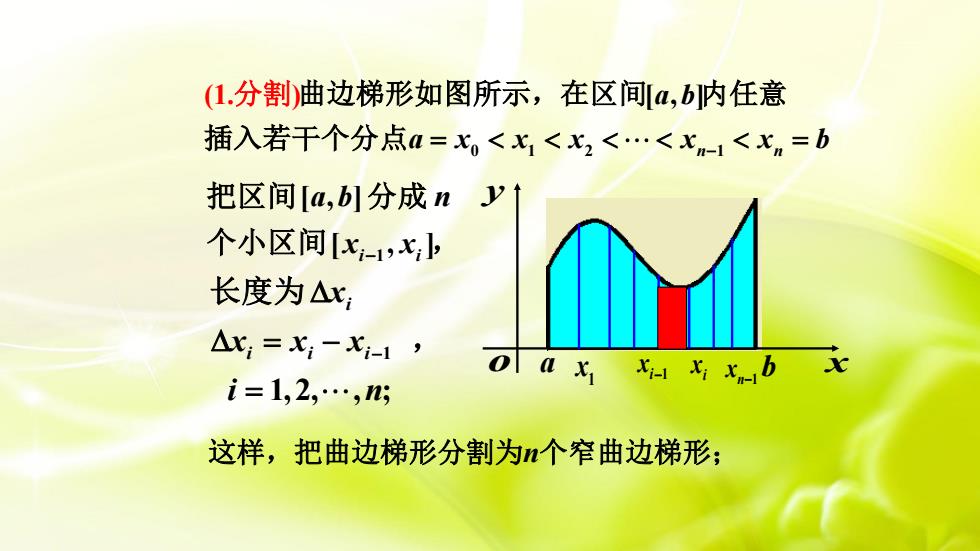
1 [ , ] [ , ] i i a b n x x − 把区间 分成 个小区间 , a b x yo i x 1 x i 1 x − n 1 x − 这样,把曲边梯形分割为n个窄曲边梯形; 1 1,2, , ; i i i i x x x x i n − = − = 长度为 , 0 1 2 1 (1. ) [ , ] n n a b a x x x x x b = = − 曲边梯形如图所示,在区间 内任意 插入若干个分点 分割

(2.近似)在每个小区间[x;-1,x,|上任取一点,以[x;-1,x,为底,f()为高的小矩形的面积近似窄曲边梯形的面积,则yAA, ~ f()Ax, i=1,2,.,n(3.作和)曲边梯形面积的近似值为A=Z, ~Zf(s,)Ax;oabx5xi x-1X(4.取极限)当分割无限加细时,设所有小区间长度的最大值a=max[Ax,Ax,,..Ax,,当a→时,曲边梯形面积为 A=limf(5,)Ax;1-0i=l
1 1 ( ) n n i i i i i A A f ξ x = = = (3.作和)曲边梯形面积的近似值为 1 2 , max (4. , } 0 ) { , n λ = → x x x λ 当分割无限加细时 设所有小区间长度的 最大值 ,当 取极限 时, i n i i A = f x = → lim ( ) 1 0 曲边梯形面积为 1 ( ) 2. [ , ] i i i x x ξ 近似 在每个小区间 − 上任取一点 , ( ) 1,2, , A f i i i = ξ x i n 1 [ , ] ( ) i i i x x f ξ 以 − 为底, 为高的小矩形的 面积近似窄曲边梯形的面积,则 a b x y o i x 1 x i 1 x − n 1 x − i

实例2(求变速直线运动的路程)设某物体作直线运动,已知速度v=v(t)是时间间隔[T,T1上t的一个连续函数,且v(t)≥0,求物体在这段时间内所经过的路程思路:以不变代变把整段时间分割成若干小段每小段上速度看作不变,求出各小段的路程再相加,便得到路程的近似值,最后通过对时间的无限细分过程求得路程的精确值
实例2 (求变速直线运动的路程) 设某物体作直线运动,已知速度v = v(t)是 时间间隔[ , ] T1 T2 上 t 的一个连续函数,且 v(t) 0,求物体在这段时间内所经过的路程. 思路:以不变代变 把整段时间分割成若干小段, 每小段上速度看作不变,求出各小段的路程再 相加,便得到路程的近似值,最后通过对时间 的无限细分过程求得路程的精确值.