
第六节函数图形的描绘一、曲线的渐近线函数图形的描绘
第六节 函数图形的描绘 一、曲线的渐近线 二、函数图形的描绘

第三章微分中值定理与导数的应用渐近线一当曲线y=f(x)上的一动点M沿着曲线移向无穷点时如果点M到某定直线L的趋向于零那么直线L就距离定义称为曲线y=f(x)的一条渐近线t或为“纵坐标差”例如:双曲线=1a2b2x y有渐近线=0但抛物线y=×?无渐近线第六节函数图形的描绘
第六节 函数图形的描绘 第三章 微分中值定理与导数的应用 一、渐近线 有渐近线 x a ± y b = 0 例如: 或为“纵坐标差” 但抛物线y = x 2无渐近线. 定义 当曲线 y = f(x) 上的一动点 M 沿着曲线移向无穷点时, 如果点 M 到某定直线 L 的 趋向于零,那么直线 L 就 称为曲线 y = f(x) 的一条渐近线. 距离
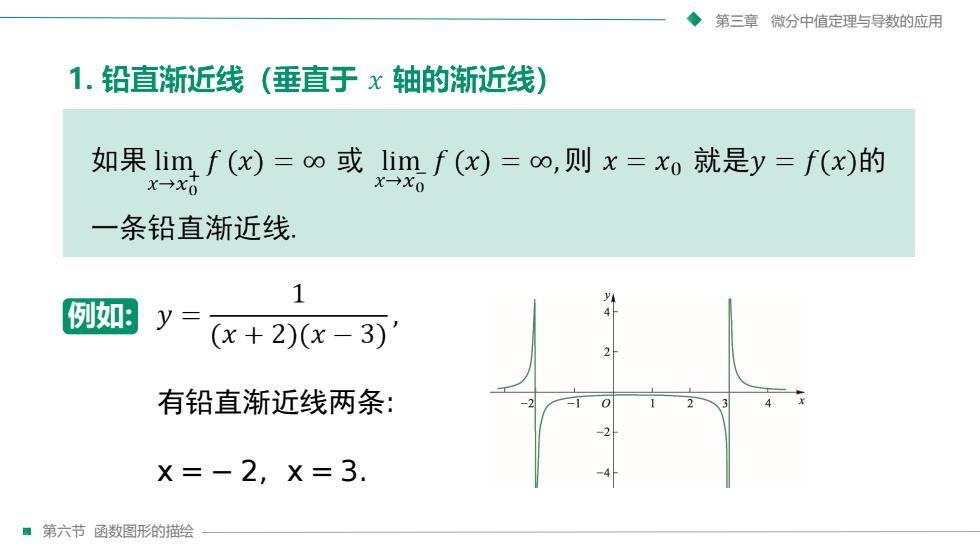
第三章微分中值定理与导数的应用1.铅直渐近线(垂直于x轴的渐近线)如果limf(x)=80或limf(x)=0,则x=xo就是y=f(x)的x-xo-xo一条铅直渐近线1J例如:V(x + 2)(x - 3)有铅直渐近线两条:0X = - 2, x = 3.第六节函数图形的描绘
第三章 微分中值定理与导数的应用 第六节 函数图形的描绘 例如: 有铅直渐近线两条: x = − 2, x = 3
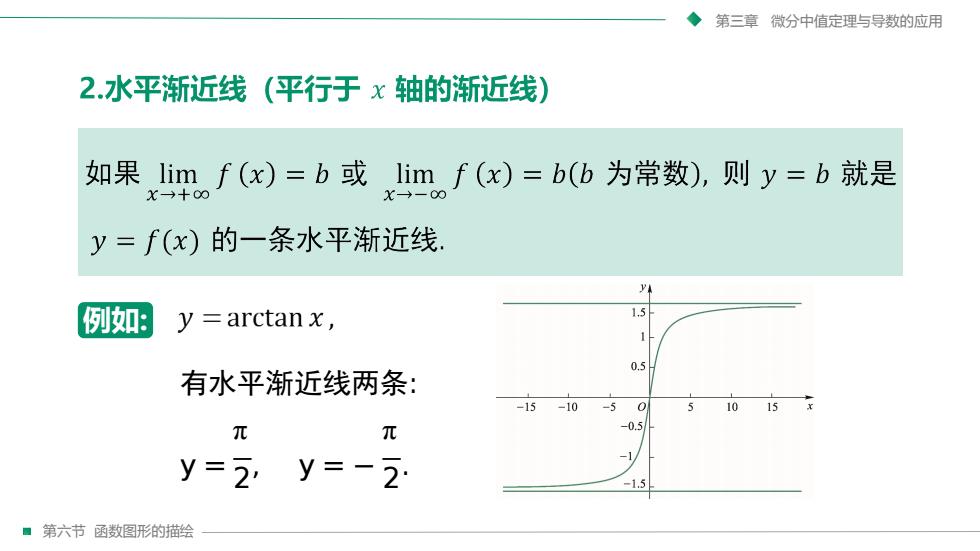
第三章微分中值定理与导数的应用2.水平渐近线(平行于x轴的渐近线)如果limf(x)=b或limf(x)=b(b为常数),则y=b就是x-8xy=f(αx)的一条水平渐近线y1.5例如:y =arctan x,0.5有水平渐近线两条:41015-15-10-5050.5元元y = 2'y = - 2.第六节函数图形的描绘
第三章 微分中值定理与导数的应用 第六节 函数图形的描绘 例如: 有水平渐近线两条: y = π 2 , y = − π 2
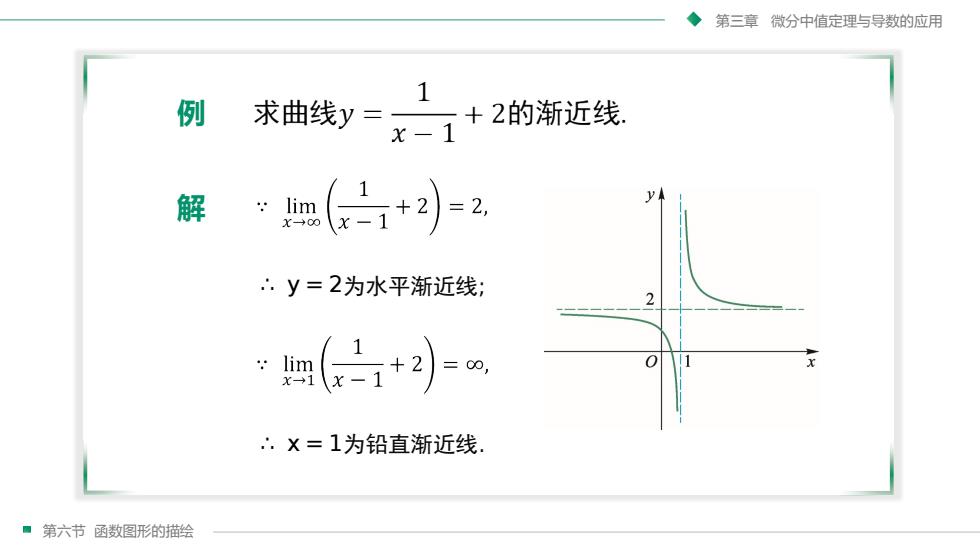
第三章微分中值定理与导数的应用1例求曲线y+2的渐近线x-11V解lim:2+-1X-00x:y=2为水平渐近线;20xlim8x→1X:×=1为铅直渐近线第六节函数图形的描绘
第六节 函数图形的描绘 第三章 微分中值定理与导数的应用 解 例 ∴ y = 2为水平渐近线; ∴ x = 1为铅直渐近线