
三、反函数 例3判断下列正误 (1)y=sinx(-0<x<+o)不存在反函数 (2)y=mx(-号三x≤号)有反函数,记作y=esinx.xc-l,yc (3) y=cosx(0≤x≤π)有反函数,记作y=arccosx,x∈-l,,y∈[0,π (④)y=mx(-受<x经)有反函数,记作y=cmxe(风m,ye(仁号受 (5)y=cotx(0<r<π)有反函数,记作y=arccotx,.x∈(-o,+o,ye(0,π)
三、反函数 例 3 判断下列正误 (1) y = sin x ( ) −∞ < < +∞ x 不存在反函数 (2) y x = sin ( 2 2 x π π − ≤≤ )有反函数,记作 y xx = ∈− arcsin , [ 1,1], [ ,] 2 2 y π π ∈ − (3) y = cos x(0 ≤ ≤x π )有反函数,记作 y xx = arccos , [ 1,1] ∈ − , y ∈[0, ] π (4) y x = tan ( 2 2 x π π − << )有反函数,记作 y xx = ∈ −∞ +∞ arctan , ( , ), ( ,) 2 2 y π π ∈ − (5) y = cot x( 0 < <x π )有反函数,记作 y xx = arccot , ( , ) ∈ −∞ +∞ , y ∈(0, ) π
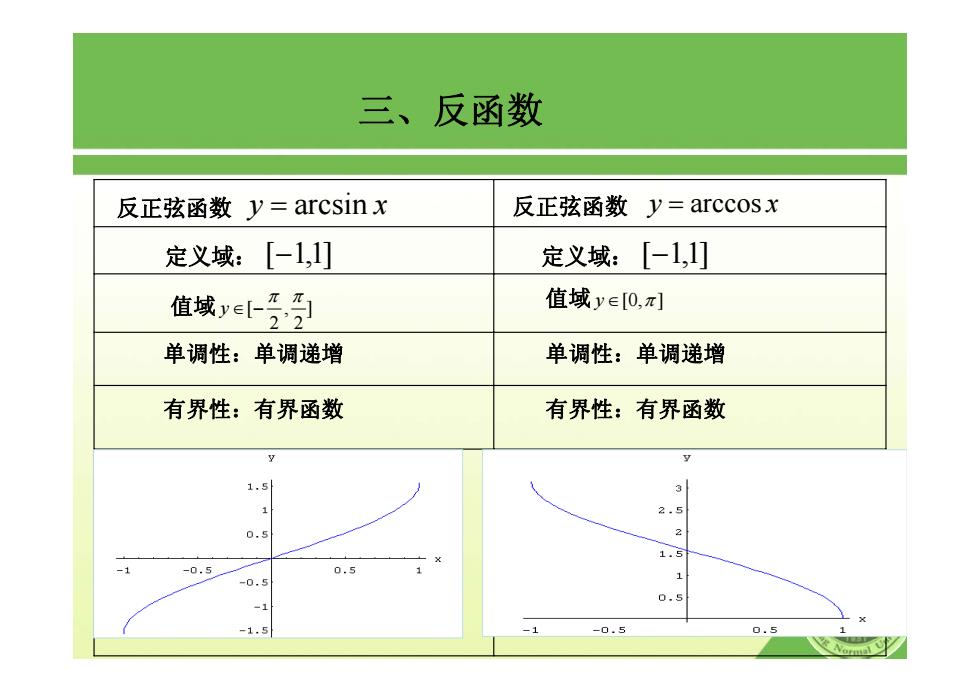
三、反函数 反正弦函数y=arcsinx 反正弦函数y=arccosx 定义域:[-1,1] 定义域:[-1,1] 值域ye 值域ye0,π] 单调性:单调递增 单调性:单调递增 有界性:有界函数 有界性:有界函数 y 1.5 2.5 0.5 1.5 -0.5 0.5 -0.5 0.5 -1 -1.5 -1 -0.5 5 y
三、反函数 值域 [ ,] 2 2 y π π ∈ − 单调性:单调递增 有界性:有界函数 值域 y ∈[0, ] π 单调性:单调递增 有界性:有界函数 反正弦函数 y = arcsin x 反正弦函数 y = arccos x 定义域: [−1,1] 定义域: [−1,1]

0,+0 三、反函数 反正切函数y=arctanx 反余切函数y=arc cotx 定义域:(-0,+o) 定义域:(-0,+o) 值域ye 值域ye(0,π) 单调性:单调递增 单调性:单调递增 有界性:有界函数 有界性:有界函数 0.5 -0.5
三、反函数 值域 ( ,) 2 2 y π π ∈ − 单调性:单调递增 有界性:有界函数 值域 y ∈(0, ) π 单调性:单调递增 有界性:有界函数 反正切函数 y = arctan x 反余切函数 y = arc cot x −∞ +∞ , 定义域:(−∞ +∞ , ) 定义域:(−∞ +∞ , )

五、复合函数与初等函数 1.复合函数 有关注记 (1)如果函数y=f(m)的定义域D, 注记1:如果u=p(x)的值全部落在 (2)函数u=o(x)的定义域D,值域 y=f)的定义域内,则复合函y=几p(x] 为W2, 的定义域与u=p(x)的定义域相同. 注记2:如果u=(x)的值部分地落在 (3)且W,cD y=f)的定义域内,则复合函数y=f几p(x] 那么y通过u的联系也是x的函数.称 的定义域是u=p(x)的定义域的子集 这个函数是由y=fw)及u=o(x)复合 注记3:如果u=p(x)的值全部落在y=f(m 而成的,称为复合函数.记作 的定义域外,则不能构成复合函数, y=flo(x)] 其中u叫做中间变量
五、复合函数与初等函数 1.复合函数 有关注记 (1)如果函数 y = f (u)的定义域 D1, ( 2 )函数 u = ϕ(x) 的定义域 D2,值域 为 W2 , (3)且 W2 ⊂ D1 那么 y 通过 u 的联系也是 x的函数.称 这个函数是由 y fu = ( ) 及u x = ϕ( )复合 而成的,称为复合函数.记作 y = f [ϕ(x)] 其中 u叫做中间变量. 注记 1:如果u x = ϕ( )的值全部落在 y f = ( ) u 的定义域内,则复合函 y = f [ϕ(x)] 的定义域与u x = ϕ( )的定义域相同. 注记 2:如果u x = ϕ( )的值部分地落在 y fu = ( ) 的定义域内,则复合函数 y = f [ϕ(x)] 的定义域是u x = ϕ( )的定义域的子集 注记 3:如果u x = ϕ( )的值全部落在 y f = ( ) u 的定义域外,则不能构成复合函数

五、复合函数与初等函数 基本初等函数 (1) 幂函数 y=x“(u为实常数) (2)指数函数 y=a'(a>0,a≠1,a为常数) (3)对数函数 y=log。x(a>0,a≠l,a为常数) (4)三角函数 y=sin x,y=cosx,y=tanx,y=cotx,y=secx,y=cscx (5)反三角函数:y=arcsinx,y=arccosx,y=arctanx,y=arccotx 初等函数:由常数及基本初等函数经过有限次的四则运算及有限复合步骤 所构成并且可以用一个式子表示的函数 叫做初等函数
五、复合函数与初等函数 x 基本初等函数 (1) 幂函数 (μ为实常数 ) μ y = x (2) 指数函数 y a (a 0,a 1,a为常数) x = > ≠ (3) 对数函数 y log x(a 0,a 1,a为常数) = a > ≠ (4) 三角函数 y = sin x, y = cos x, y = tan x, y = cot x, y = sec x, y = csc x (5) 反三角函数: y = arcsin , arccos , arctan , arccot x y === x y x y x 初等函数:由常数及基本初等函数经过有限次的四则运算及有限复合步骤 所构成并且可以用 一个式子表示的函数 叫做初等函数