
§1.2 数列的极限 主要内容 一、概念的引入 二、数列的定义 三、数列的极限 四、数列极限的性质
§1.2 数列的极限 一、概念的引入 二、数列的定义 三、数列的极限 四、数列极限的性质 主要内容
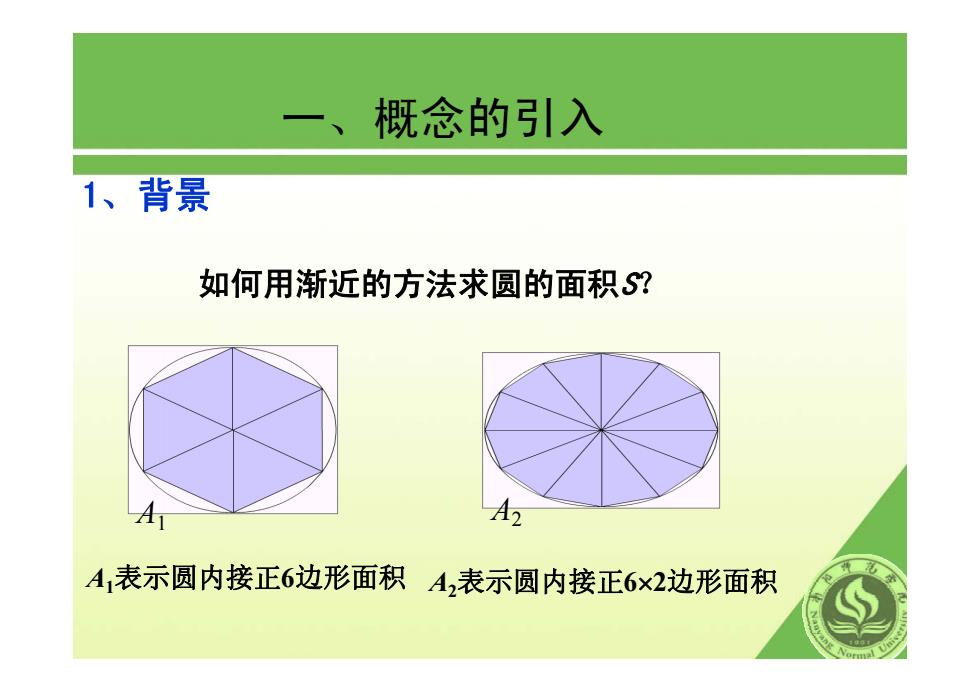
一、概念的引入 1、背景 如何用渐近的方法求圆的面积S? A灯 A2 A1表示圆内接正6边形面积A,表示圆内接正6×2边形面积
一、概念的引入 1、背景 如何用渐近的方法求圆的面积 S? A 1 A 1表示圆内接正 6边形面积 A 2 A 2表示圆内接正 6 × 2边形面积
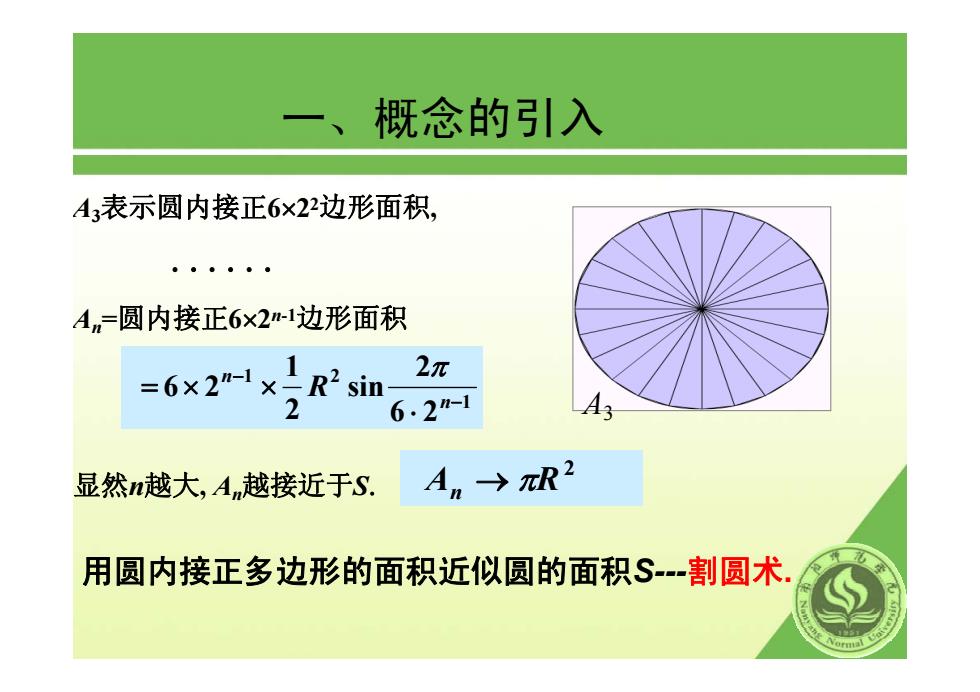
概念的引入 A3表示圆内接正6×22边形面积, 00。。0● Am=圆内接正6×2-1边形面积 =6x2xIR'sim 2π 2 6.2m- 43 显然越大,An越接近于S. An→元R2 用圆内接正多边形的面积近似圆的面积S-割圆术
一、概念的引入 A 3 用圆内接正多边形的面积近似圆的面积S---割圆术. A 3表示圆内接正 6 × 2 2边形面积, ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ A n =圆内接正 6 × 2 n-1边形面积 显然 n越大, A n越接近于 S. 1 1 2 6 2 2 sin 2 1 6 2 − − ⋅ = × × n n R π 2 A n → πR

二、数列的极限的概念 数列的概念, 数列的特点及几何意义 如果按照某一法则,可以得到第一个数x,第 数列的特征: 二个数x,,这样依次序排列着,使得对应于任何 ①由数组成的序列 一个正整数n有一个确定的数x,那么这列有序的 ②这个序列中的每个数都编了号 数x,水2,Xn,…就叫做数列. ③序列中有无限多个成员 数列中的每一项叫做数列的项,第n项x叫做数 数列的几何意义: 数列对应着数轴上一个点列.可看作 的通项.数列x,x,x…简记为{x.也可简记为 一动点在数轴上依次取x,X2,…,Xn,… 数列x 在数列x}中任意抽取无限多项并保持这些项在原 数列与函数的关系:数列可以看作自变量 数列中的先后次序,这样得到的一个数列称为原数列 为正整数的函数:xf(m它的定义城 是全体正整数 {x的子数列
二、数列的极限的概念 数列的概念. 如果按照某一法则,可以得到第一个数 1 x , 第 数列的特点及几何意义 数列的特征: ①由数组成的序列 ② 这个序列中的每个数都编了号 ③序列中有无限多个成员 数列的几何意义: 数列对应着数轴上一个点列.可看作 一动点在数轴上依次取 1 2 ,,,,. n xx x " " 数列与函数的关系: 数列可以看作自变量 为正整数的函数: x n =f (n)它的定义域 是全体正整数. 二个数 2 x , ⋅⋅⋅,这样依次序排列着,使得对应于任何 一个正整数 n 有一个确定的数 , n x 那么这列有序的 数 1 2, , ,, n xx x ⋅⋅⋅ ⋅⋅⋅就叫做数列. 数列中的每一项叫做数列的 项,第 n 项 n x 叫做数 的通项. 数列 1 2, , ,, n xx x ⋅⋅⋅ ⋅⋅⋅简记为{xn} .也可简记为 数列 n x . 在数列{xn}中任意抽取无限多项并保持这些项在原 数列中的先后次序, 这样得到的一个数列称为原数列 {x n}的子数列

二、数列极限的概念 发现 结论 ①当n→o时,xn= (-无限接近常数1 当n无限增大时,数列①②③的通项 n ②当n→0时,通项x,=”无限接近常数1 x无限接近于一个确定的常数 n+1 ③当n→o时,通项xn= 2分 无限接近常数0 数列④的通项不接近于任何常数 ④当n→0时,x,=(←1)+不接近于任何常数
二、数列极限的概念 ① 当 n → ∞ 时, +( 1)n n n x n − = 无限接近常数 1 ② 当 n → ∞ 时,通项 1 n n x n = + 无限接近常数 1 ③ 当 n → ∞ 时,通项 1 2 n n x = 无限接近常数 0 ④当 n → ∞ 时, 1 ( 1)n n x + = − 不接近于任何常数 发 现 结 论 当 n 无限增大时,数列①②③的通项 n x 无限接近于一个确定的常数 数列④的通项不接近于任何常数