
向量组及其线性组合 一、n维向量概念及表示方法 定义:n个有次序的数a,a,.,a,所组成的数组称为n维向量,这n个数称为该 向量的n个分量,第i个数a称为第i个分量。 实向量:分量全为实数的向量。 复向量:分量为复数的向量。 表示方法: n维向量写成一行,称为行向量,也就是行矩阵,通常用a,b,α',B等表 示,如: a=(a,a,.,a) n维向量写成一列,称为列向量,也就是列矩阵,通常用a,b,a,B等表示, 如: a a) 向量的维数:向量中元素的个数叫做向量的维数。 注:1·行向量和列向量总被看作是两个不同的向量: 2.行向量和列向量都按照矩阵的运算法则进行运算: 3.当没有明确说明是行向量还是列向量时,都当作列向量 二、向量空间 将线性代数中的向量的概念与解析几何中介绍的向量的概念在n≤3下比 较:
向量组及其线性组合 一、n维向量概念及表示方法 定义: n 个有次序的数 1 2 , n a a a L 所组成的数组称为n 维向量,这 n 个数称为该 向量的n 个分量,第i 个数 i a 称为第i 个分量。 实向量:分量全为实数的向量。 复向量:分量为复数的向量。 表示方法: n 维向量写成一行,称为行向量,也就是行矩阵,通常用 , , , T T T T a b a b 等表 示,如: 1 2 ( , , , ) T n a = a a a L n 维向量写成一列,称为列向量,也就是列矩阵,通常用a b, , , a b 等表示, 如: 1 2 n a a a a æ ö ç ÷ ç ÷ = ç ÷ ç ÷ è ø M 向量的维数:向量中元素的个数叫做向量的维数。 注:1.行向量和列向量总被看作是两个不同的向量; 2.行向量和列向量都按照矩阵的运算法则进行运算; 3.当没有明确说明是行向量还是列向量时,都当作列向量. 二、向量空间 将线性代数中的向量的概念与解析几何中介绍的向量的概念在 n £ 3下比 较:
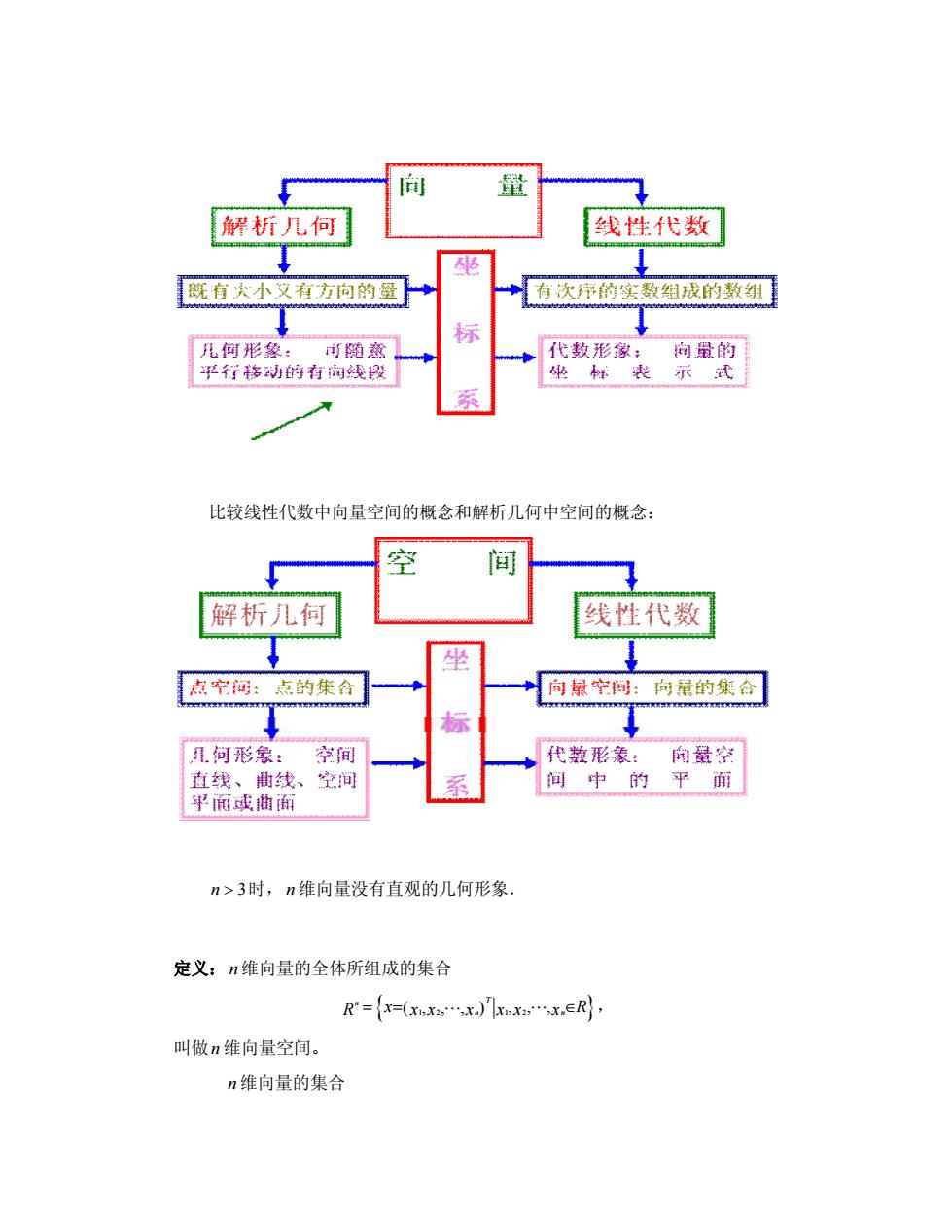
量 解析几何 线性代数 既有天小有方向的量 有次序的实数组成的数组 何形 代数形像: 量的 了多动的相长北安 坐装示式 系 比较线性代数中向量空间的概念和解析几何中空间的概念: 间 解析儿何 线性代数 坐 点窄御:点的集合 向宁间:向的集合 几何形象: 学间 代数形象 向最空 直线、线、空间 系 间中的 面 平面或曲面 n>3时,n维向量没有直观的儿何形象。 定义:n维向量的全体所组成的集合 R=x=xxR 叫做n维向量空间。 n维向量的集合
比较线性代数中向量空间的概念和解析几何中空间的概念: n > 3时, n 维向量没有直观的几何形象. 定义: n 维向量的全体所组成的集合 { ( 1 2 , , , ) 1 2 , , , } n n n T R = x R = Î x x x L x x x L , 叫做n 维向量空间。 n 维向量的集合

π={x=(xx.x)lax,+a2x:++ax=b 叫做n维向量空间R中的n-1维超平面。 三、向量、向量组与矩阵 向量组:若干个同维数的列向量(或同维数的行向量)所组成的集合叫做向量组。 注:一个m×n的矩阵可以看作是n个m维列向量构成的向量组,同样也可以看 作是m个n维行向量构成的向量组。反之,n个m维列向量构成的向量组可以看 成是一个m×n的矩阵,m个n维行向量构成的向量组也可以看成是一个m×n的 矩阵,所以,向量的很多性质可以通过矩阵来考虑。 定义:给定向量组A:a1,a,.,an,对于任何一组实数k,k,.,kn,表达式 ka+ka2+.+k.an 称为向量组A:a,a2,.,a。,的一个线性组合,k,k,.,k。,称为这个线性组合的 系数。 定义:给定向量组A:a,a,a和向量b,如果存在一组数入,2.入使 b=a1+2a2+.+元am, 则向量b是向量组A:a,a2,.,a,的线性组合,这时称向量b能由向量组 A:a1,a2,0n,线性表示。 2 1 -5 10 0 例如:B= 0 3 ,61 10 0 84= 0 (0 1 定理:向量b能由向量组A:a%,a2,am,线性表示的充分必要条件是矩阵 A=(a,a2,a)的秩等于矩阵B=(a,a,.,an,b)的秩。 定义:设有两个向量组A:a,a2,.,an及B:B,B,B,若B组中的每个向量 都能由向量组A现象表示,则称向量组B能由向量组A线性表示,若向量组A与
{ ( 1 2 , , , )n 1 1 2 2 n n } T p = x b = x x x L a x +a x +L+ = a x 叫做n 维向量空间 n R 中的 n -1维超平面。 三、向量、向量组与矩阵 向量组:若干个同维数的列向量(或同维数的行向量)所组成的集合叫做向量组。 注:一个m n ´ 的矩阵可以看作是 n 个 m 维列向量构成的向量组,同样也可以看 作是m 个n 维行向量构成的向量组。反之,n 个 m 维列向量构成的向量组可以看 成是一个m n ´ 的矩阵,m 个n 维行向量构成的向量组也可以看成是一个 m n ´ 的 矩阵,所以,向量的很多性质可以通过矩阵来考虑。 定义:给定向量组 1 2 : , , , , A a a a L m ,对于任何一组实数 1 2 , , , , m k k k L 表达式 1 1 2 2 m m k a + k k a a + + L 称为向量组 1 2 : , , , , A a a a L m 的一个线性组合, 1 2 , , , , m k k k L 称为这个线性组合的 系数。 定义:给定向量组 1 2 : , , , , A a a a L m 和向量b ,如果存在一组数 1 2 , , , m l l l L ,使 1 1 2 2 m m b = l a + l a + + L l a , 则向量 b 是向量组 1 2 : , , , , A a a a L m 的线性组合,这时称向量 b 能由向量组 1 2 : , , , , A a a a L m 线性表示。 例如: 1 2 3 4 2 1 0 0 0 5 0 1 0 0 , , , , 3 0 0 1 0 0 0 0 0 1 b e e e e æ ö æ ö æ ö æ ö æ ö ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ - ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ = = = = = ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø è ø è ø è ø 定理:向量 b 能由向量组 1 2 : , , , , A a a a L m 线性表示的充分必要条件是矩阵 1 2 ( , , , ) A = a a a L m 的秩等于矩阵 1 2 ( , , , , ) B b = a a a L m 的秩。 定义:设有两个向量组 1 2 : , , , A a a a L m及 1 2 : , , , B s b b b L ,若 B 组中的每个向量 都能由向量组 A 现象表示,则称向量组 B 能由向量组 A 线性表示,若向量组 A与

向量组B能相互线性表示,则称这两个向量组等价。 定理:向量组B:B,B,B能由向量组A:a,a,.,a线性表示的充分必要条 件是矩阵A=(a,a2,.,a)的秩等于矩阵(A,B)=(a1,a2,.,am,B,B2,.,B)的 秩,即R(A)=R(AB) 推论:向量组A:a,4,an与向量组B:月,B2,.,B等价的充分必要条件是 R(A)=R(B)=R(A,B),其中A和B是向量组A和B所构成的矩阵。 1 1Y 例1:设a,= 24-1 0 .b= 证明向量b能由向量组a,42,4,线 2 3 0 性表示,并求出表达式。 1 3 2) (3 例2:设a,= 1 ,42= 1 ,= b= 2 证明向量组a,a,与向 1 -1 3 1 2 量组,b,b等价。 定理:设向量组B:B,B,.,B,能由向量组A:a,a2,.,a线性表示,则 RB.B2,.,B,)≤Ra,a2,.,am) 总结:向量组B:,b,b,能由向量组4a,a,an线性表示, 一有矩阵K,使B=AK 一方程AX=B有解 R(A)=R (A,B) =R(A)≥R(B) 例3:设n维向量组A:a,2,.,an构成n×m矩阵A=(a,a,aw),n阶单位矩 阵E=(%,已2,.,en)的列向量叫做n维单位坐标向量组。证明:n维单位坐标向量 组e,e,能由向量组A线性表示的充分必要条件是R(A)=n
向量组 B 能相互线性表示,则称这两个向量组等价。 定理:向量组 1 2 : , , , B s b b b L 能由向量组 1 2 : , , , A a a a L m线性表示的充分必要条 件是矩阵 1 2 ( , , , ) A = a a a L m 的秩等于矩阵 1 2 1 2 ( , ) ( , , , , , , , ) A B = a a L L am s b b b 的 秩,即 R(A) = R(A B, ) 推论:向量组 1 2 : , , , A a a a L m 与向量组 1 2 : , , , B s b b b L 等价的充分必要条件是 R(A) = = R(B) R(A B, ),其中 A和 B 是向量组 A和 B 所构成的矩阵。 例 1:设 1 2 3 1 1 1 1 1 2 1 0 , , , 2 1 4 3 2 301 a a a b æ ö æ ö æ ö æ ö ç ÷ ç ÷ ç ÷ ç ÷ - ç ÷ ç ÷ ç ÷ ç ÷ = = = = ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø è ø è ø ,证明向量 b 能由向量组 1 2 3 a , , a a 线 性表示,并求出表达式。 例 2:设 1 2 1 3 1 1 , 1 1 1 3 a a æ ö æ ö ç ÷ ç ÷ - ç ÷ ç ÷ = = ç ÷ ç ÷ ç ÷ ç ÷ è- ø è ø , 123 2 1 3 0 1 1 , , 1 0 2 1 2 0 b b b æ ö æ ö æ ö ç ÷ ç ÷ ç ÷ - ç ÷ ç ÷ ç ÷ = = = ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø è ø ,证明向量组 1 2 a a, 与向 量组 1 2 3 b , , b b 等价。 定理:设向量组 1 2 : , , , B b b b L s能由向量组 1 2 : , , , A a a a L m线性表示,则 1 2 ( , , , ) R b b b L s £ 1 2 ( , , , ) R a a a L m 总结: 1 2 1 2 , ,., , ,., B l m 向量组 :b b b能由向量组A:a a a 线性表示 , K B AX B R(A) R A B R A R B Û Û = Û = Þ ³ 有矩阵 ,使 =AK 方程 有解 ( , ) ( ) ( ) 例 3:设n 维向量组 1 2 : , , , A m a a a L 构成n m´ 矩阵 1 2 ( , , , ) A m = a a a L ,n 阶单位矩 阵 1 2 ( , , , ) E n = e e e L 的列向量叫做n 维单位坐标向量组。证明:n 维单位坐标向量 组 1 2 , , , n e e e L 能由向量组 A线性表示的充分必要条件是 R( ) A n =

四、向量组的线性相关性 定义:给定向量组A:a,a2,.,心,如果存在不全为零的数k,k2,.,k,使 k4,+ka2+.+knan=0,则称向量组A:a1,a2,.,n是线性相关的。否则称它 线性无关。 注 (1)m=1时,即对于只有一个向量的向量组,若该向量为零,则是线性相关的, 若该向量不为零,则是线性无关的。 (2)m=2时,即对于含有两个向量的向量组,若它们线性相关,则这两个向 量对应分量成比例。 (3)m=3时,即含有三个向量的向量组,若它们线性相关,则这三个向量共面。 结论: (1)若n个向量构成的向量组线性相关,则在该向量组中至少有一个向量能由 其余的n-1个向量线性表示。 (2)如果向量组A中有某个向量能由其余的m-1个向量线性表示,则向量组 A是线性相关的。 定理:向量组a,a,.,a.线性相关的充分必要条件是它所构成的矩阵 A=(a,a,a)的秩小于向量个数m,向量组线性相关的充分必要条件是 R(A)=m 例4:试讨论n维单位坐标向量组的线性相关性 1 0 2 例5:已知a,= ,讨论向量组a,a,a,及向量组a,a的线性 5 相关性。 例6:已知向量组a,a,a,线性无关,b=a+a,b,=a,+a,b=a,+a,试证:向 量组b,b,b线性无关
四、向量组的线性相关性 定义:给定向量组 1 2 : , , , A a a a L m,如果存在不全为零的数 1 2 , m k, ,k k L ,使 1 1 2 2 0 m m k a + k k a a +L+ = ,则称向量组 1 2 : , , , A a a a L m是线性相关的。否则称它 线性无关。 注: (1)m = 1时,即对于只有一个向量的向量组,若该向量为零,则是线性相关的, 若该向量不为零,则是线性无关的。 (2) m = 2 时,即对于含有两个向量的向量组,若它们线性相关,则这两个向 量对应分量成比例。 (3)m = 3时,即含有三个向量的向量组,若它们线性相关,则这三个向量共面。 结论: (1) 若n 个向量构成的向量组线性相关,则在该向量组中至少有一个向量能由 其余的n -1个向量线性表示。 (2) 如果向量组 A中有某个向量能由其余的 m -1个向量线性表示,则向量组 A是线性相关的。 定理: 向 量组 1 2 , , , a a a L m 线 性相 关的 充分 必要条件 是它 所构 成的 矩阵 1 2 ( , , , ) A a a am = L 的秩小于向量个数 m ,向量组线性相关的充分必要条件是 R( ) A m= 例 4:试讨论n 维单位坐标向量组的线性相关性 例 5:已知 1 2 3 1 0 2 1 , 2 , 4 1 5 7 a a a æ ö æ ö æ ö ç ÷ ç ÷ ç ÷ = = = ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø è ø ,讨论向量组 1 2 3 a , , a a 及向量组 1 2 a a, 的线性 相关性。 例 6:已知向量组 1 2 3 a , , a a 线性无关, 1 1 2 2 2 3 3 3 1 b = a + a ,b = a + a , , b = + a a 试证:向 量组 1 2 3 b , , b b 线性无关