
内蒙古科技大学2009/2010学年第二学期 《线性代数》考试试题A卷 课程号:68132105 考试方式:闭卷 使用专业、年级:09级各专业 任课教师:张景、唐俊等 考试时间: 备注:所有答案写在答题纸上 一、选择题(共7题,每题4分,共28分) 4 1.设A,B都是n阶方阵,下面结论一定正确的是(C)】 (A)(AB)-=A-B- (B)AB=BA (C)(A+B)=AT+B (D)4+B=+B 2.若矩阵A经过初等变换化为矩阵B,则必有(A) (A)r(A)=r(B)(B)|A=B (C)A-=B- (D)AT=B ==== 3.向量组A:a1,a2,a,(s22)线性无关的充分必要条件是(A) (A)当且仅当k1=k2=.=k,=0时,ka1+k2a2+.+k,a,=0成立 (B)其中至少有一个向量不能用其余s-1个向量线性表示 (C)a1,a2,4,中任意两个向量都不成比例 (D)a41,a2,.a,均不是零向量 4.设A,B,C均为n阶矩阵,下面(A)一定成立 (A)(A+B)+C=(C+B)+A (B)(A+BC=CA+CB (C)(AB)C=B(AC) (D)(AB)C=(AC)B 5.关于n阶对称矩阵Q,下列说法正确的是(A)》 (A)O=0 (B)OO=E (c)lo>o (D)O'=0- 1 24 6.矩阵A 1-25的秩为(B) 1102 (A)1 (B)2 (C)0 (D)4
内蒙古科技大学 2009/2010 学年第二学期 《线性代数》考试试题 A 卷 课程号:68132105 考试方式:闭卷 使用专业、年级:09 级各专业 任课教师:张景、唐俊等 考试时间: 备 注:所有答案写在答题纸上 一、选择题(共 7 题,每题 4 分,共 28 分) 1.设 A , B 都是n 阶方阵,下面结论一定正确的是(C ) (A) -1 -1 -1 (AB) = A B (B) AB = BA (C) T T T (A + B) = A + B (D) A+ B = A + B 2.若矩阵 A 经过初等变换化为矩阵 B ,则必有(A ) (A)r(A) = r(B) (B) A = B (C) -1 -1 A = B (D) T T A = B 3. 向量组 : , , ( 2) A a1 a2 Las s ³ 线性无关的充分必要条件是(A ) (A)当且仅当 0 k1 = k2 = L = ks = 时, 0 k1a1 + k2a2 +L+ ksas = 成立 (B)其中至少有一个向量不能用其余s -1个向量线性表示 (C)a a Las , , 1 2 中任意两个向量都不成比例 (D)a a Las , , 1 2 均不是零向量 4.设 A,B,C 均为 n 阶矩阵,下面(A )一定成立 (A)(A + B)+ C = (C + B) + A (B)(A + B)C = CA + CB (C)(AB)C = B(AC) (D)(AB)C = (AC)B 5.关于 n 阶对称矩阵Q,下列说法正确的是(A) (A)Q = Q T (B)Q Q = E T (C) Q > 0 (D) * -1 Q = Q 6.矩阵 1 2 4 1 2 5 1 10 2 A æ ö ç ÷ = - ç ÷ ç ÷ è ø 的秩为(B) (A)1 (B)2 (C)0 (D)4 学 生 班 级 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 学 生 学 号:□ □ □ □ □ □ □ □ □ □ □ □ 学 生 姓 名:_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ . . . . . . 装 订 线 . . . 装 订 线 . . . 装 订 线 . . . . 试 卷 须 与 答 题 纸 一 并 交 监 考 教 师 . . . . 装 订 线 . . . 装 订 线 . . . 装 订 线 . . . . .
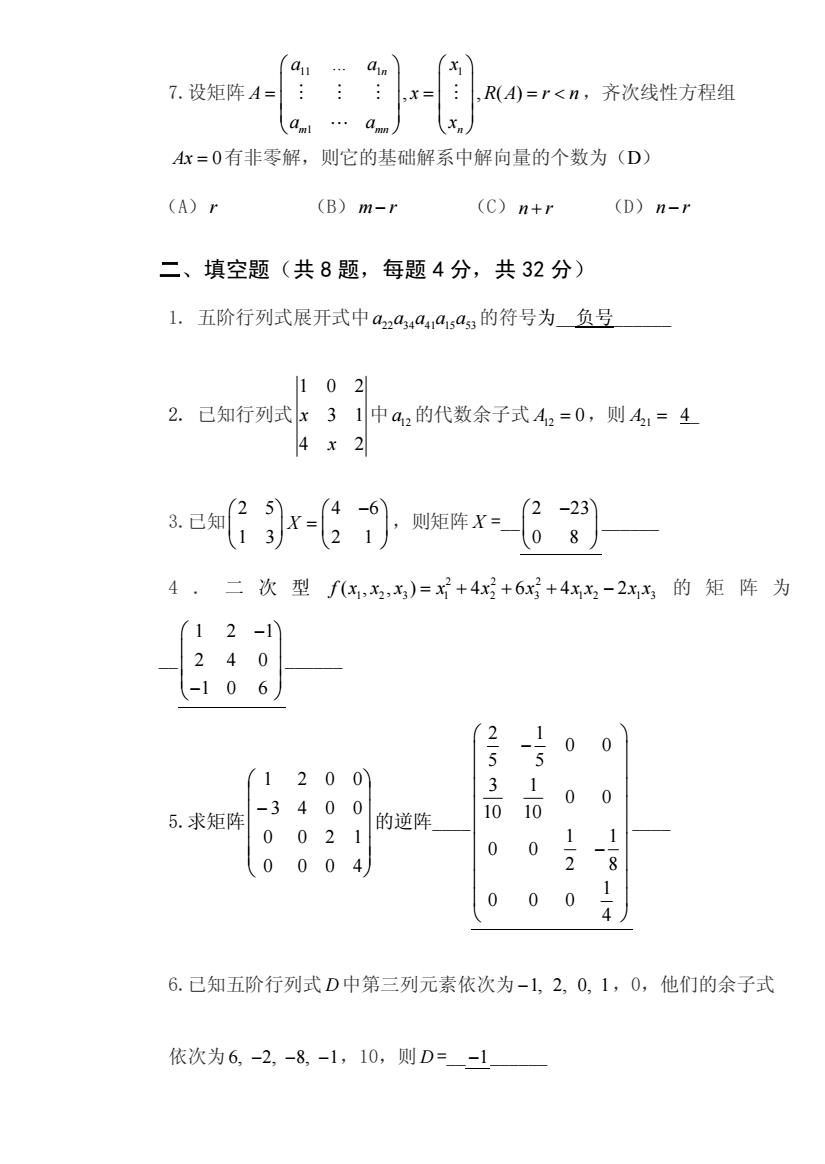
a1 7.设矩阵A ,R(4)=r<n,齐次线性方程组 Ax=0有非零解,则它的基础解系中解向量的个数为(D)》 (A)r (B)m-r (C)n+r (D)n- 二、填空题(共8题,每题4分,共32分 1.五阶行列式展开式中a,aa4,a:的符号为_负号 102 2.己知行列式x31中a2的代数余子式A2=0,则A=4 4x2 4.二 次型f,,)=+4x+6x+4xx-2x的矩阵为 d 5 5 0 1200 3 、1 5.求矩阵 -3400 0 0 的逆阵 10 10 0021 0 0 0004 2 0 00 6.已知五阶行列式D中第三列元素依次为-1,2,0,1,0,他们的余子式 依次为6,-2,-8,-1,10,则D=-1
7.设矩阵 11 1 1 1 . , , ( ) n m mn n a a x A x R A r n a a x æ ö æ ö ç ÷ ç ÷ = = = < ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø M M M M L ,齐次线性方程组 Ax = 0有非零解,则它的基础解系中解向量的个数为(D) (A)r (B)m r - (C)n r + (D)n r - 二、填空题(共 8 题,每题 4 分,共 32 分) 1. 五阶行列式展开式中 22 34 41 15 53 a a aaa 的符号为_负号_ 2. 已知行列式 102 3 1 4 2 x x 中 12 a 的代数余子式 12 A = 0,则 A21 = 4_ 3.已知 2 5 4 6 1 3 2 1 X æ ö æ ö - ç ÷ = ç ÷ è ø è ø ,则矩阵 X =_ 2 23 0 8 æ ö - ç ÷ è ø _ 4 . 二 次 型 222 1 2 3 1 2 3 1 2 1 3 f (x , x , x ) = x + + 4x 6x + - 4 2 x x x x 的 矩 阵 为 _ 1 2 1 240 1 0 6 æ ö - ç ÷ ç ÷ ç ÷ è ø - _ 5.求矩阵 ÷ ÷ ÷ ÷ ÷ ø ö ç ç ç ç ç è æ - 0 0 0 4 0 0 2 1 3 4 0 0 1 2 0 0 的逆阵_ 2 1 0 0 5 5 3 1 0 0 10 10 1 1 0 0 2 8 1 0 0 0 4 æ ö - ç ÷ - è ø _ 6.已知五阶行列式 D 中第三列元素依次为-1, 2, 0, 1,0,他们的余子式 依次为6, -2, - - 8, 1,10,则 D =_ -1_
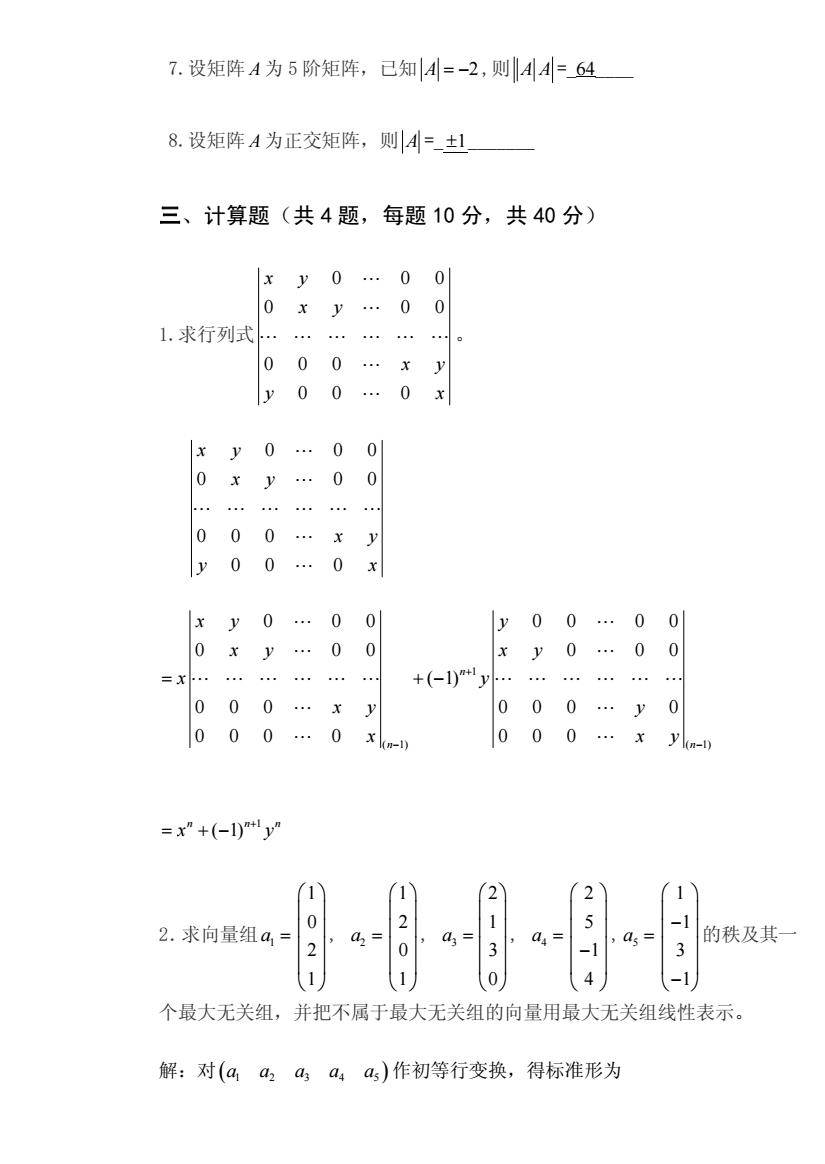
7.设矩阵A为5阶矩阵,已知A=-2,则AA=64 8.设矩阵A为正交矩阵,则A=±1 三、计算题(共4题,每题10分,共40分) |xy0.00 0xy.00 1.求行列式.。 000.xy y00.0x xy0.00 0xy.00 . 000.xy y00.0x xy0.0 0 y 00.0 0 xy.0 0 xy0.00 =x . . 0 00. x y 0 0 0.y0 000.0 xko-i) 000.xym- =x"+(-1)+1y 2 2.求向量组( 0 2 的秩及其 -1 1 1 0 个最大无关组,并把不属于最大无关组的向量用最大无关组线性表示 解:对(aaa,a4a)作初等行变换,得标准形为
7.设矩阵 A 为 5 阶矩阵,已知 A = -2 ,则 A A =_64_ 8.设矩阵 A 为正交矩阵,则 A =_ ±1_ 三、计算题(共 4 题,每题 10 分,共 40 分) 1.求行列式 0 0 0 0 0 0 000 0 0 0 x y x y x y y x L L L L L L L L L L 。 0 0 0 0 0 0 000 0 0 0 x y x y x y y x L L LLLLLL L L 1 ( 1) ( 1) 0 0 0 0 0 0 0 0 0 0 0 0 0 ( 1) 0 0 0 0 0 0 0 0 0 0 0 000 n n n x y y x y x y x y x y y x x y + - - = + - L L L L LLLLL L LLLLLL L L L L 1 ( 1) n n n x y + = + - 2.求向量组 1 a = 1 0 2 1 æ ö ç ÷ ç ÷ ç ÷ ç ÷ è ø , 2 a = 1 2 0 1 æ ö ç ÷ ç ÷ ç ÷ ç ÷ è ø , 3 a = 2 1 3 0 æ ö ç ÷ ç ÷ ç ÷ ç ÷ è ø , 4 a = 2 5 1 4 æ ö ç ÷ ç ÷ ç ÷ - ç ÷ è ø , 5 a = 1 1 3 1 æ ö ç ÷ - ç ÷ ç ÷ ç ÷ è ø - 的秩及其一 个最大无关组,并把不属于最大无关组的向量用最大无关组线性表示。 解:对(a1 a2 3 a a a 4 5 ) 作初等行变换,得标准形为

10010 0103 -1 001-11 00000 由此可得一个最大无关组为{a,a,4} 且a4=a+3a2-a3,a5=a-a, 元x+x2+x=1 3.求非齐次线性方程组 x+元x+x3=元 +x+x=2 (1)有唯一解:(2)无解:(3)无穷解,并在有无穷解时求通解。 211 解:令系数矩阵行列式为零,即1入1=0,解得1=1或入=-2 11 于是原方程组当入≠1且入≠-2时有唯一解。 当入=-2时,系数矩阵的秩小于增广矩阵的秩,此时方程组无解。 当入=1时,原方程组即x+x2+x=1 0 得对应的齐次方程组的基础解系为 0 0(0 0 于是原方程组此时的通解为x=G +c21 -1 其中,C,为任意常数 0 03 0-11) 4.矩阵A= -101 求正交矩阵P,使得P-AP=A。 10
1 0 0 1 0 0 1 0 3 1 0 0 1 1 1 0 0 0 0 0 æ ö ç ÷ - - è ø 由此可得一个最大无关组为 1 2 3 {a , a a, } 且 4 1 2 3 a = a + - 3a a , 5 3 2 a = - a a 3.求非齐次线性方程组 1 2 3 1 2 3 2 1 2 3 x x x 1 x x x x x x l l l l l ì + + = ï í + + = ï î + + = (1)有唯一解;(2)无解;(3)无穷解,并在有无穷解时求通解。 解:令系数矩阵行列式为零,即 1 1 1 1 0 1 1 l l l = ,解得l =1或l = -2 于是原方程组当l ¹ 1且l ¹ -2 时有唯一解。 当l = -2 时,系数矩阵的秩小于增广矩阵的秩,此时方程组无解。 当l =1时,原方程组即 1 2 3 x + x x + =1 得对应的齐次方程组的基础解系为 1 0 0 1 0 0 æ ö æ ö ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø 、 。 于是原方程组此时的通解为 1 2 1 0 1 0 1 1 0 0 3 x c c æ ö æ ö æ ö - ç ÷ ç ÷ ç ÷ = + + - ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø è ø ,其中 1 2 c c, 为任意常数。 4.矩阵 0 1 1 1 0 1 1 1 0 A æ ö - ç ÷ = -ç ÷ ç ÷ è ø ,求正交矩阵 P ,使得 1 P AP - = L

|21-1 解:令11-1=(1-1)2(1+2)=0,解得1=1或1=-2。 -1-1 0 当入=1时,解得对应的特征向量 0 当入=-2时,解得对应的特征向量为 1 -1 6 2 6 再单位化,即得所求正交矩阵P 0 口口 52 6366 303 3 1 0 0 且满足P-AP=A= 0 1 0 0 0 -2
解:令 2 1 1 1 1 ( 1) ( 2) 0 1 1 l l l l l - - = - + = - - ,解得l =1或l = -2 。 当l =1时,解得对应的特征向量为 1 0 0 1 1 1 æ ö æ ö ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø 、 ,正交化为 1 1 2 0 1 1 1 2 æ ö -ç ÷ æ ö ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø ç ÷ è ø 、 当l = -2 时,解得对应的特征向量为 1 1 1 æ ö ç ÷ ç ÷ ç ÷ è ø - 。 再单位化,即得所求正交矩阵 2 6 3 2 6 3 6 3 0 3 3 2 6 3 2 6 3 P æ ö ç ÷ - = - è ø , 且满足 1 1 0 0 0 1 0 0 0 2 P AP - æ ö ç ÷ = L = ç ÷ ç ÷ è ø - 学 生 班 级 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 学 生 学 号:□ □ □ □ □ □ □ □ □ □ □ □ 学 生 姓 名:_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ . . . . . . 装 订 线 . . . 装 订 线 . . . 装 订 线 . . . . 试 卷 须 与 答 题 纸 一 并 交 监 考 教 师 . . . . 装 订 线 . . . 装 订 线 . . . 装 订 线 . . . . .