
3-1矩阵的初等变换与线性方程组 1.消元法解线性方程组 问题的提出:前面我们看到,对于有n个未知数,n个方程的线性方程组,我们 可以通过克拉默法则来求解。而现实世界中经常有这样的方程组,在个未知数 的方程组中,只有m个方程,若m<n,则方程组的系数构不成行列式,所以不 能通过克拉默法则求解,那么,我们今天来讨论这类方程的求解问题。 2x-x-x+x=2 例如:求解线性方程组{x+x2-2x+x=4 4x-6x2+2x3-2x4=4 2x-x3-x+x=2 解:利用消元法: x+x-2x+x=4 4x-6x2+2x-2x4=4 [x+x2-2x+x4=4 2%-为-为+x=2 4x-6x2+2x-2x=4 x+x-2x+x=4 2x-2-为+=2 2x-3x2+x3-x=2 +为2-2x+x=4 -3x2+3x-x,=-6 -2x2+2x-2x=0 x+x2-2x+x=4 3-为+x=0 x4=-3 用“回代”的方法求出解:于是解得 x=x3+4 书=为+3 x4=-3 其中x为任意取值.或令x=c,方程组的解可记作
3-1 矩阵的初等变换与线性方程组 1. 消元法解线性方程组 问题的提出:前面我们看到,对于有 n 个未知数,n 个方程的线性方程组,我们 可以通过克拉默法则来求解。而现实世界中经常有这样的方程组,在 n 个未知数 的方程组中,只有 m 个方程,若 m n < ,则方程组的系数构不成行列式,所以不 能通过克拉默法则求解,那么,我们今天来讨论这类方程的求解问题。 例如:求解线性方程组 1 234 1 2 3 4 1 2 3 4 2 2 2 4 4 6 2 2 4 x xxx x x x x x x x x ì - - + = ï í + - + = ï - + - = î 解:利用消元法: 1 234 1 2 3 4 1 2 3 4 2 2 2 4 4 6 2 2 4 x x x x x x x x x x x x ì - - + = ï í + - + = ï - + - = î 1 2 3 4 1 234 1 2 3 4 2 4 2 2 4 6 2 2 4 x x x x x x x x x x x x ì + - + = ï í - - + = ï - + - = î 1 2 3 4 1 234 1 2 3 4 2 4 2 2 2 3 2 x x x x x x x x x x x x ì + - + = ï í - - + = ï - + - = î 1 2 3 4 2 3 4 2 3 4 2 4 3 3 6 2 2 2 0 x x x x x x x x x x ì + - + = ï í- + - = - ï- + - = î 1 2 3 4 2 3 4 4 2 4 0 3 x x x x x x x x ì + - + = ï í - + = ï î = - 用“回代”的方法求出解: 于是解得 1 3 2 3 4 4 3 3 x x x x x ì = + ï í = + ï î = - 3 其中x 为任意取值. 3 或令x c = ,方程组的解可记作

c+4) 2. 矩阵的初等变换 上述变换过程中,实际上只对方程组的系数和常数项进行变换,未知数并未参加 运算,即在求解方程组得过程就是对增广矩阵进行行变换的过程。变换可以归结 为三种。即: 1、互换两行:5《5 2、数乘某行:,'k 3、某行的k倍加到另一行:,+如 而且,这三种变换都是可逆的,而且逆变换与原变换类型相同, 万《)逆变换)《: 万:逆变换,专 r+如逆变换r-: 我们将这三种变换叫做矩阵的初等行变换。 类似的,我们可以定义矩阵的初等列变换, 矩阵的初等行变换和初等列变换统称作矩阵的初等变换。 定义:如果矩阵A经过有限次初等行变换变成矩阵B就称矩阵A与B行等价,记 作A二B。 定义:如果矩阵A经过有限次初等列变换变成矩阵B就称矩阵A与B列等价,记 作AB。 定义:如果矩阵A经过有限次初等变换变成矩阵B就称矩阵A与B等价,记作 AB。 等价关系的性质: (1)反身性:A~A (2)对称性:若A~B,则B~A
1 2 3 4 4 3 , 3 x c x c x x c x æ ö æ ö + ç ÷ ç ÷ + ç ÷ ç ÷ = = ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø - 即 1 2 3 4 1 4 1 3 , 1 0 0 3 x x x c x x æ ö æ ö æ ö ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ = = + ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø è ø - 2. 矩阵的初等变换 上述变换过程中,实际上只对方程组的系数和常数项进行变换,未知数并未参加 运算,即在求解方程组得过程就是对增广矩阵进行行变换的过程。变换可以归结 为三种。即: 1、互换两行: i j r r « 2、数乘某行: i r k ´ 3、某行的k 倍加到另一行: i j r + kr 而且,这三种变换都是可逆的,而且逆变换与原变换类型相同, i j r r « 逆变换 ; i j r r « i r k ´ 逆变换 1 i r k ´ i j r + kr 逆变换 i j r - kr 我们将这三种变换叫做矩阵的初等行变换。 类似的,我们可以定义矩阵的初等列变换, 矩阵的初等行变换和初等列变换统称作矩阵的初等变换。 定义:如果矩阵 A 经过有限次初等行变换变成矩阵 B 就称矩阵 A 与 B 行等价,记 作 ~ r A B 。 定义:如果矩阵 A经过有限次初等列变换变成矩阵 B 就称矩阵 A与 B 列等价,记 作 ~ c A B 。 定义:如果矩阵 A 经过有限次初等变换变成矩阵 B 就称矩阵 A 与 B 等价,记作 A B ~ 。 等价关系的性质: (1)反身性: A A ~ (2)对称性:若 A B ~ ,则 B A ~
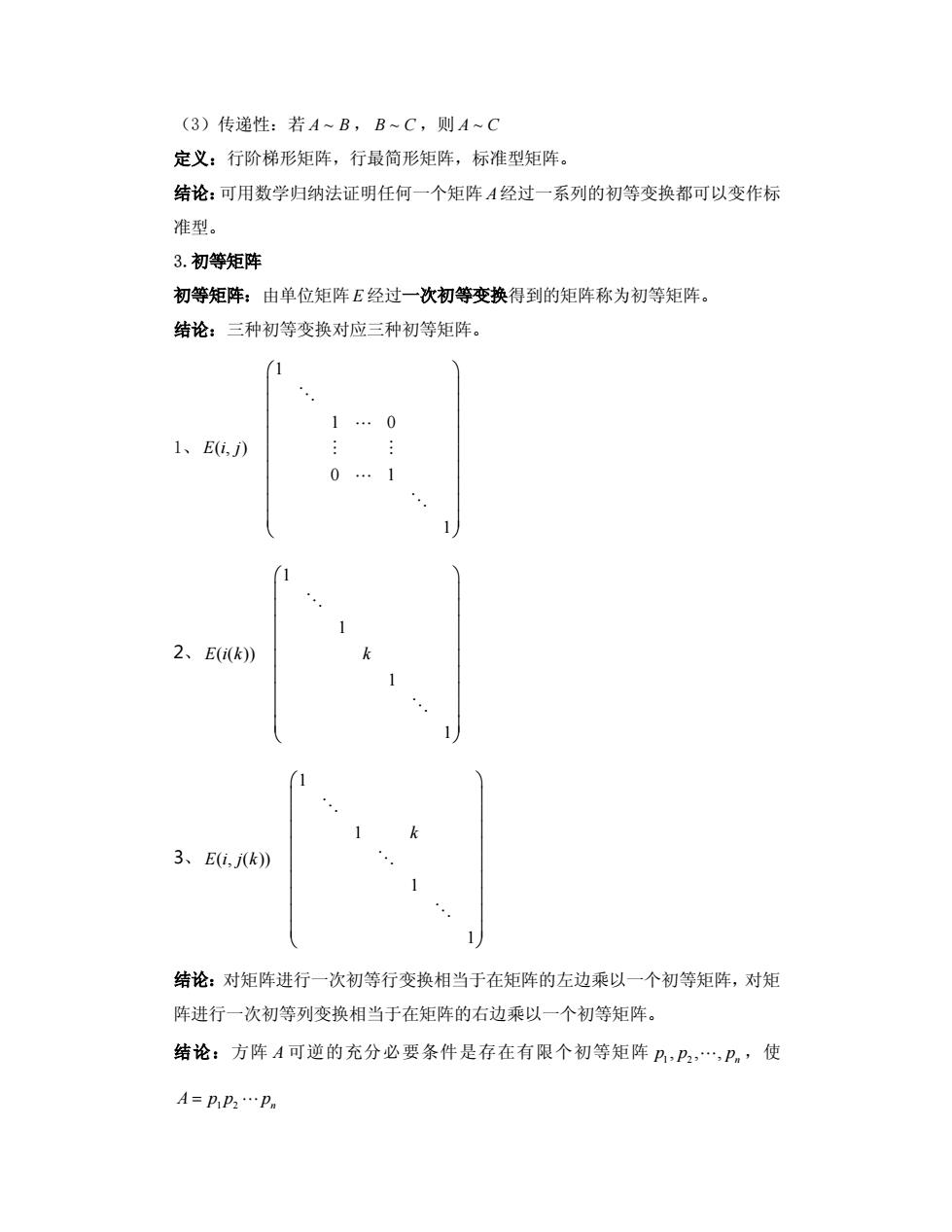
(3)传递性:若A~B,B~C,则A~C 定义:行阶梯形矩阵,行最简形矩阵,标准型矩阵。 结论:可用数学归纳法证明任何一个矩阵A经过一系列的初等变换都可以变作标 准型。 3.初等矩阵 初等矩阵:由单位矩阵E经过一次初等变换得到的矩阵称为初等矩阵。 结论:三种初等变换对应三种初等矩阵, 1.0 1、E6,) 0.1 (1 2、E(ik) 3、E,jk)》 1 结论:对矩阵进行一次初等行变换相当于在矩阵的左边乘以一个初等矩阵,对矩 阵进行一次初等列变换相当于在矩阵的右边乘以一个初等矩阵。 结论:方阵A可逆的充分必要条件是存在有限个初等矩阵A,P2,.,P。,使 A=P P:P
(3)传递性:若 A B ~ , B C~ ,则 A C~ 定义:行阶梯形矩阵,行最简形矩阵,标准型矩阵。 结论:可用数学归纳法证明任何一个矩阵 A经过一系列的初等变换都可以变作标 准型。 3.初等矩阵 初等矩阵:由单位矩阵 E 经过一次初等变换得到的矩阵称为初等矩阵。 结论:三种初等变换对应三种初等矩阵。 1、 E(i j , ) 1 1 0 0 1 1 æ ö ç ÷ è ø O L M M L O 2、 E(i k( )) 1 1 1 1 k æ ö ç ÷ è ø O O 3、 E(i, j k( )) 1 1 1 1 k æ ö ç ÷ è ø O O O 结论:对矩阵进行一次初等行变换相当于在矩阵的左边乘以一个初等矩阵,对矩 阵进行一次初等列变换相当于在矩阵的右边乘以一个初等矩阵。 结论:方阵 A 可逆的充分必要条件是存在有限个初等矩阵 1 2 , , , n p p p L ,使 A 1 2 n = p p p L

4.初等矩阵的应用 定理:设A与B为m×n矩阵,那么: 1)A~B的充分必要条件是存在m阶可逆矩阵P,使PA=B 2)A~B的充分必要条件是存在n阶可逆矩阵Q,使AQ=B 3)A~B的充分必要条件是存在m阶可逆矩阵P和n阶可逆矩阵Q,使PAQ=B 推论:方阵A可逆的充分必要条件是AE 推论:若方阵A可逆,则将矩阵(A:E)经过初等行变换,将A变换为E后,则E 将变为。 推论:若方阵A可逆,则将矩阵(A:B)经过初等行变换,将A变换为E后,则B 将变为AB。 (51-2)1-3 例:用初等变换解矩阵方程:AX=X+B,其中A=231,B=22 3103-1 例:将矩阵(A:B)利用初等变换化为行阶梯形,再化为行最简形,最后化为标准形 1-22-1 1 2-480 -24-23 .8s 3 3-60-6 4 在本课程中,我们只讨论行变换,列变换我们一般不用,那么形如XA=B方程 组如何解呢,我们可以将方程组得两端同时取转置。 3-2矩阵的秩 定义(k阶子式):在m×n的矩阵A中,任取k行与k列,位于这些行列交叉的 元素不改变它们在矩阵A中所处的位置次序而得到的k阶行列式,称为矩阵A的
4.初等矩阵的应用 定理:设 A与 B 为m n ´ 矩阵,那么: 1) ~ r A B 的充分必要条件是存在m 阶可逆矩阵 P ,使 PA B = 2) ~ c A B 的充分必要条件是存在n 阶可逆矩阵Q,使 AQ B = 3)A B ~ 的充分必要条件是存在 m 阶可逆矩阵 P 和n 阶可逆矩阵Q,使 PAQ B = 推论:方阵 A可逆的充分必要条件是 ~ r A E 推论:若方阵 A可逆,则将矩阵(A E: )经过初等行变换,将 A变换为 E 后,则 E 将变为 1 A - 。 推论:若方阵 A可逆,则将矩阵(A B: ) 经过初等行变换,将 A 变换为 E 后,则 B 将变为 1 A B- 。 例:用初等变换解矩阵方程: AX = + X B ,其中 5 1 2 1 3 2 3 1 , 2 2 3 1 0 3 1 A B æ - - ö æ ö ç ÷ ç ÷ = = ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø - 例:将矩阵(A B: )利用初等变换化为行阶梯形,再化为行最简形,最后化为标准形 1 2 2 1 1 2 4 8 0 2 , 2 4 2 3 3 3 6 0 6 4 A B æ - - ö æ ö ç ÷ ç ÷ - ç ÷ ç ÷ = = ç - - ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è - - ø è ø 例:求矩阵 0 2 1 3 0 2 2 3 0 é ù - ê ú - ê ú ë û - 的逆矩阵。 在本课程中,我们只讨论行变换,列变换我们一般不用,那么形如 XA B = 方程 组如何解呢,我们可以将方程组得两端同时取转置。 3-2 矩阵的秩 定义(k 阶子式):在m n ´ 的矩阵 A 中,任取 k 行与 k 列,位于这些行列交叉的 元素不改变它们在矩阵 A 中所处的位置次序而得到的k 阶行列式,称为矩阵 A 的

k阶子式。 100 举例:A=010 110 定义(矩阵秩):设在矩阵A中有一个不等于0的k阶子式D,且所有k+1阶子 式(如果存在的话)都等于0,那么D称为A的最高阶非零子式(最高阶非零子 式不一定唯一),数k称为矩阵A的秩,记作R(A),并规定零矩阵的秩为O。 例:①求上例矩阵A的秩。(降秩矩阵)》 (121 例:②求矩阵A=231 的秩。(满秩矩阵) 4713 一方阵A可逆,可逆矩阵的秩等于其阶数n,称为满秩矩阵,不可逆矩阵的 秩小于其阶数n,称为降秩矩阵。 (2-103 -2 031-25 例:③求矩阵B= 的秩。(行阶梯形矩阵) 0004-3 00000Js 一行阶梯形矩阵的秩就等于其非零行的行数,即等于阶梯的个数。 定理:矩阵经初等变换,秩不变。(若两个矩阵等价,则它们的秩相等。) -求秩方法:A~行阶梯形矩阵B,则R(A)=R(B)=B的非零行的行数。 32050Y 例:④求矩阵4236-1 的秩,并求一个最高阶非零子式。 2015-3 16-4-14 12-11 例:⑤设A=32元-1已知R(4)=2,求元,4的值。 5634 1-22 1 2 -48 0 例:⑥设A= ,b= 求A,B=(A,b)的秩。 -2 4 -2 23 3 6 0 6/
k 阶子式。 举例: 3 3 1 1 1 0 0 1 0 1 0 0 ´ ÷ ÷ ÷ ø ö ç ç ç è æ A = 定义(矩阵秩):设在矩阵 A中有一个不等于 0 的 k 阶子式 D,且所有 k +1阶子 式(如果存在的话)都等于 0,那么 D 称为 A的最高阶非零子式(最高阶非零子 式不一定唯一),数k 称为矩阵 A 的秩,记作 R A( ),并规定零矩阵的秩为 0。 例:①求上例矩阵 A1的秩。(降秩矩阵) 例:②求矩阵 3 3 4 7 1 2 3 1 1 2 1 ¸ ÷ ÷ ÷ ø ö ç ç ç è æ A = 的秩。(满秩矩阵) ——方阵 An´n 可逆,可逆矩阵的秩等于其阶数n ,称为满秩矩阵,不可逆矩阵的 秩小于其阶数n ,称为降秩矩阵。 例:③求矩阵 4 5 0 0 0 0 0 0 0 0 4 3 0 3 1 2 5 2 1 0 3 2 ´ ÷ ÷ ÷ ÷ ÷ ø ö ç ç ç ç ç è æ - - - - B = 的秩。(行阶梯形矩阵) ——行阶梯形矩阵的秩就等于其非零行的行数,即等于阶梯的个数。 定理:矩阵经初等变换,秩不变。(若两个矩阵等价,则它们的秩相等。) ——求秩方法:A~行阶梯形矩阵 B,则 R(A)=R(B)=B 的非零行的行数。 例:④求矩阵 3 2 0 5 0 3 2 3 6 1 2 0 1 5 3 1 6 4 1 4 A æ ö ç ÷ - - = - è ø - - 的秩,并求一个最高阶非零子式。 例:⑤设 ÷ ÷ ÷ ø ö ç ç ç è æ - - = m l 5 6 3 3 2 1 1 2 1 1 A 已知 R(A) = 2 ,求l, m 的值。 例:⑥设 ÷ ÷ ÷ ÷ ÷ ø ö ç ç ç ç ç è æ = ÷ ÷ ÷ ÷ ÷ ø ö ç ç ç ç ç è æ - - - - - - - = 4 3 2 1 , 3 6 0 6 2 4 2 3 2 4 8 0 1 2 2 1 A b ,求 A, B = (A,b)的秩