《高等数学》课程教学资源（课件讲稿）第十一章 曲线积分与曲面积分_1103格林公式及其应用

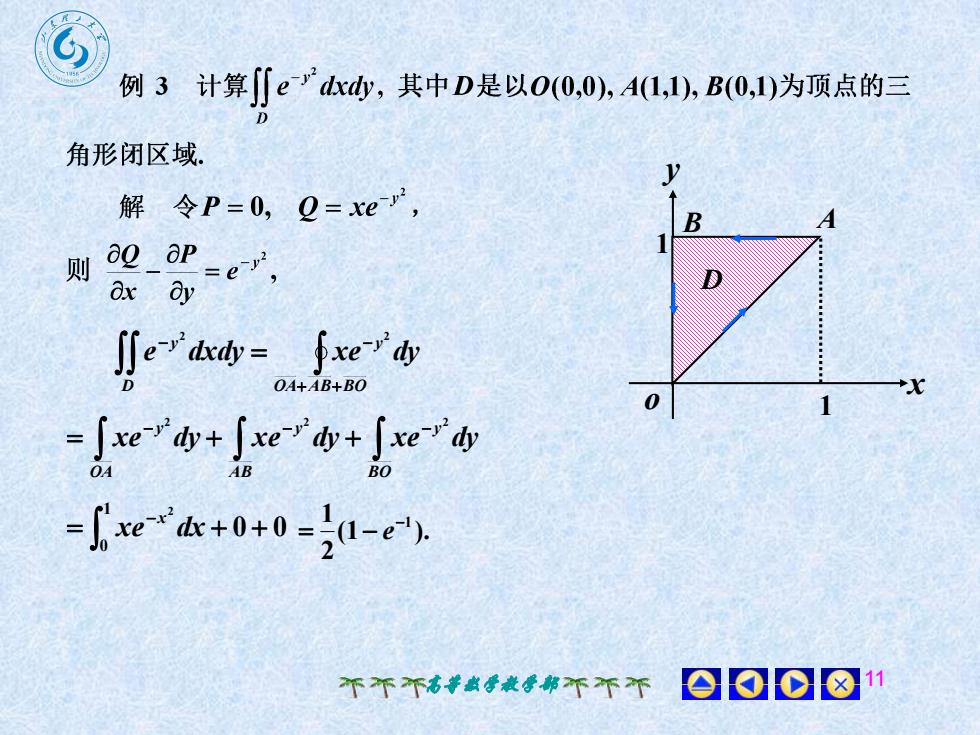
例 3 计算[[e-"dxdy,其中 D是以0(0,0), A(1,1), B(0,1)为顶点的三D角形闭区域y军 令P= 0, Q=xe-r解ABaQ ap则R..R.Ei.0DaxdyJe" dxdy -fxe-"'dyDOA+AB+BOtx1J xe-"dy + I xe-"'dy+ I xe-"dyAB0ABO-f'xe-"dx+0+0 -;(a-e"),000811个不不高数学教学部不不不

高等数学教学部 11 x y o B A 1 1 D        OA AB BO y D y e dxdy xe dy 2 2 0 0 1 0 2      xe dx x (1 ). 2 1 1   e          BO y AB y OA y xe dy xe dy xe dy 2 2 2

1例 4计算,xy2dy-xydx，其中 L 是圆周x2+ y2=R’依逆时针方向.解 P=-x'y, Q=xy2 P, =-x2, Q,=y2,f, xy'dy-x ydx - Jf(y" + x")dxdy = ] p- pdpdo = J" dof, p'dpD元R4R4=2元24x000812个不不高等数学教学部不不不

高等数学教学部 12    D ( y x )dxdy 2 2   L xy dy x ydx 2 2    D  dd 2        2 0 0 3 R d d 4 2 4 R    . 2 4 R  , , 2 2 P x Q y y   x  2 2 P  x y, Q  xy x y  a O a L

S例 5 计算[,(e* sin 2y-y)dx +(2e*cos 2y-100)dy, 其中 L 是单位圆x2 + y2=R2上从点A(1,0)到点B(-1,0)的上半圆周解作辅助线BA：y=0，L(e* sin 2y - y)dx +(2e* cos2y -100)dy = 0,Dx (e* sin 2y - y)dx + (2e* cos2y -100)dy0B(1,0)A(1,0)BA+- [[2e* cos2y-(2e* cos 2 y-1)]dxdy0-lad-gD元元(e* sin2y - y)dx +(2e* cos2y -100)dy 022000813个个个高等数学教学部不不不

高等数学教学部 13 x y B(1,0) O A(1,0) D L     BA x x (e sin2 y y)dx (2e cos2 y 100)dy  0,      BA L x x (e sin2 y y)dx (2e cos2 y 100)dy     D x x [2e cos2 y (2e cos2 y 1)]dxdy   D dxdy , 2        L x x (e sin2 y y)dx (2e cos2 y 100)dy . 2 0 2     