《高等数学》课程教学资源（PPT课件，上册）函数的微分

注：△y=f'(xo)△x+o(△x) dy=f'(xo)△x 当f'(xo)≠0时， lim △y=1im △y Ax->0dy △x-0f'(x0)△x △y lim =1 f(xo)Ax->0 Ax 所以△x→0时△y与dy是等价无穷小，故当△x 很小时，有近似公式 △y≈dy

山东农业大学 高等数学 主讲人：苏本堂 注: f (x0 )  0 时 , dy = f (x )x 0 ( ) ( ) 0 y = f  x x + o x y y x d lim 0   → f x x y x    =  → ( ) lim 0 0 x y f x x    =  →0 0 lim ( ) 1 =1 所以 x → 0 时 y dy 很小时, 有近似公式 x y  dy 与 是等价无穷小, 当 故当

=x)在点x可微台△=A△x+o(△x).d=f'(xo)△x· 例1求函数y=x2在x=1和=3处的微分. 解函数y=x2在x=1处的微分为 dy=(x2)Lkx=1△x=2Ax; 函数y=x2在=3处的微分为 d=(x2)儿x=3△x=6Ax. 例2求函数y=x3当x=2,△x=0.02时的微分 解先求函数在任意点x的微分， dy=(x3)'△=3x2Ax. 再求函数当x=2,Dx=0.02时的微分， dy-2,A-0.02=3x21x=2.A0.02=3×22×0.02=0.24

山东农业大学 高等数学 主讲人：苏本堂 例1 求函数y=x 2在x=1和x=3处的微分 dy=(x 2 )|x=1x=2x 函数y=x 2在x=3处的微分为 dy=(x 2 )|x=3x=6x 例2 求函数 y=x 3当x=2 x =002时的微分 y=f(x)在点x0可微y=Ax+o(x) dy= f (x0 )x  解 函数y=x 2在x=1处的微分为 解 先求函数在任意点x的微分 dy=(x 3 )x=3x 2x 再求函数当x=2 Dx=002时的微分 dy| x=2, x=0.02 =32 2 =3x 0.02=0.24 2 | x=2, x=0.02

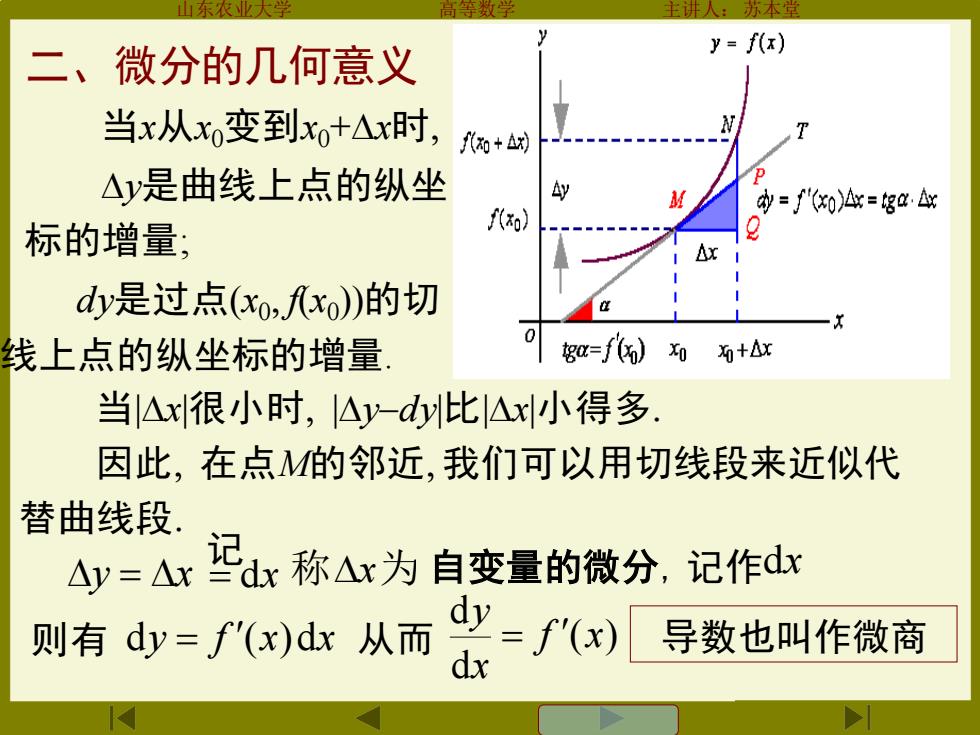
y=f(x) 二、微分的几何意义 当x从x变到x+△x时， +△的 △y是曲线上点的纵坐 y y='"0)4=gx 标的增量； dy是过点(xo,xo)的切 线上点的纵坐标的增量 0 gC=f6)和为+x 当△x很小时，△y-dy比△x小得多. 因此，在点M的邻近，我们可以用切线段来近似代 替曲线段， △y=Ardx称Ax为自变量的微分，记作d 则有dy=了x从而=了导数也叫作微酒

山东农业大学 高等数学 主讲人：苏本堂 当|x|很小时 |y−dy|比|x|小得多 因此 在点M的邻近 我们可以用切线段来近似代 替曲线段 y是曲线上点的纵坐 标的增量; dy是过点(x0  f(x0 ))的切 线上点的纵坐标的增量. 当x从x0变到x0+x时 二、微分的几何意义 则有 dy = f (x)dx 从而 ( ) d d f x x y =  导数也叫作微商 称x为 自变量的微分, 记作 dx y = x = dx 记