《高等数学》课程教学资源（PPT课件，上册）极限运算法则

第五节极限运算法则 一、无穷小运算法则 二、极限的四则运算法则 三、极限的复合运算法则 D

山东农业大学 高等数学 主讲人：苏本堂 第五节极限运算法则 一 、无穷小运算法则 二、极限的四则运算法则 三、极限的复合运算法则

山东农业大 一、无穷小运算法则 定理1.有限个无穷小的和还是无穷小. 证：考虑两个无穷小的和.设1ima=0,1imB=0, x→x0 x->xo ε>0,361>0，当0<x-x<61时，有<号 362>0,当0<x-x0<62时，有B<号 取δ=min{61,62},则当0<x-xo<6时，有 a+B≤+B|<号+号=8 因此 lim (a+B)=0. x→x0 这说明当x→xo时，+B为无穷小量 类似可证：有限个无穷小之和仍为无穷小

山东农业大学 高等数学 主讲人：苏本堂  = min 1 ,  2 , 时, 有 一、 无穷小运算法则 定理1.有限个无穷小的和还是无穷小 . 证: 考虑两个无穷小的和 . 设   0, 当 时 , 有 当 时 , 有 取 则当 0  x − x0    +    +  2 2    + =  因此 这说明当 时, 为无穷小量 . 类似可证: 有限个无穷小之和仍为无穷小

定理2有界函数与无穷小的乘积是无穷小 证明设函数u在xo的某一去心邻域{x0<x-xol<6}内 有界，即30，使当0<x-xl<6时，有M. 又设a是当xx时的无穷小，即H>0,存在6>0，使当 0<x-xo<时，有a<M. 取min{6,},则当0<x-xl<6时，有 lualua<s 这说明ua也是当x→x时的无穷小. 推论1常数与无穷小的乘积是无穷小. 推论2有限个无穷小的乘积也是无穷小

山东农业大学 高等数学 主讲人：苏本堂 设函数u在x0的某一去心邻域{x|0|x−x0 | 1 }内 有界 即M0 使当0|x−x0 |1时 有|u|M 又设是当x→x0时的无穷小 即0 存在20 使当 0|x−x0 |2时 有||/M  取=min{1  2 } 则当0|x−x0 | 时 有 |u|=|u|||  这说明u 也是当x→x0时的无穷小 证明 定理2 有界函数与无穷小的乘积是无穷小 推论2 有限个无穷小的乘积也是无穷小 推论1 常数与无穷小的乘积是无穷小

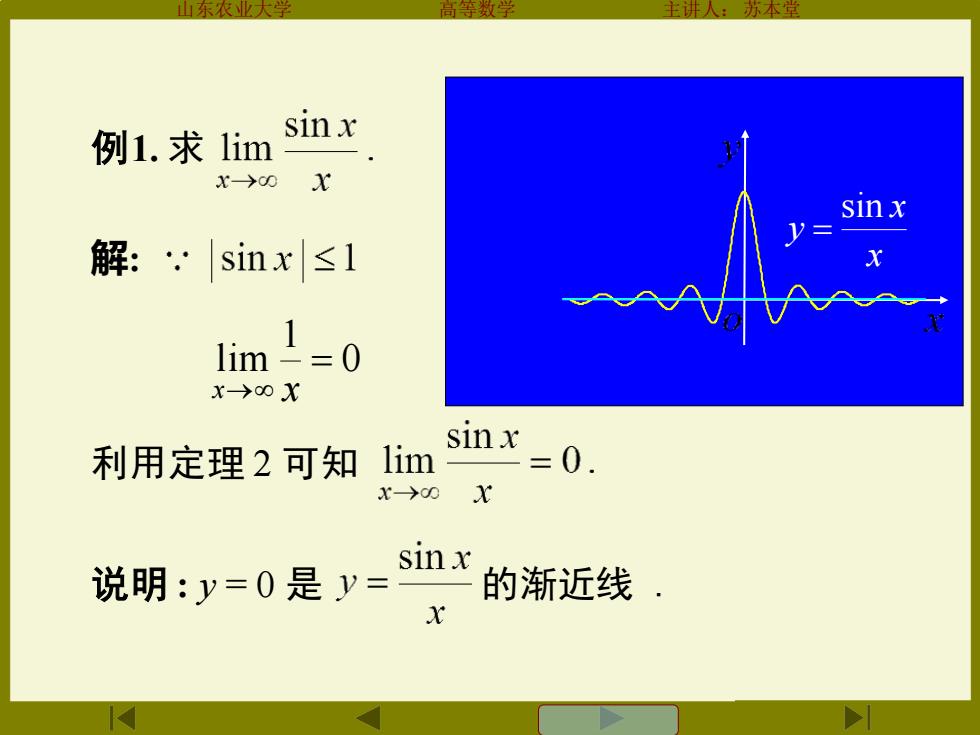
苏本堂 例1.求l1im sinx x→00 解：，sinx≤l 1im=0 x→0X sinx 利用定理2可知lim x>001X sinx 说明：y=0是y= 的渐近线

山东农业大学 高等数学 主讲人：苏本堂 例1. 求 解: 0 1 lim = x→ x 利用定理 2 可知 x x y sin = 说明 : y = 0 是 的渐近线

二、极限的四则运算运算法则 定理3 如果limx)片A,1img(x)=B,那么 (1)lim[/x)±g(x)]=limx)壮limg(x)FA±B. (2)lim fx)g(x)=lim f(x)lim g(x)=4.B. (3)lim)_lim f(x)A g(x)lim g(x)B (B0)】 推论1如果1im几x)存在，而c为常数，则 lim[c:fx)]=c-limf(x). 推论2如果limf(x)存在，而n是正整数，则 lim[fx)]"=[limf(x)]

山东农业大学 高等数学 主讲人：苏本堂 二、 极限的四则运算运算法则 (2)lim f(x)g(x)=lim f(x)lim g(x)=AB 推论1 如果lim f(x)存在 而c为常数 则 lim[cf(x)]=climf(x) 推论2 如果limf(x)存在 而n是正整数 则 lim[f(x)]n=[limf(x)]n  定理3 如果 lim f(x)=A lim g(x)=B 那么 (3) B A g x f x g x f x = = lim ( ) lim ( ) ( ) ( ) lim (B0) (1)lim[f(x)g(x)]=limf(x)limg(x)=AB