
第四章多元函数微分学 第一节 多元函数 一、空间解析几何简介 (一)空间直角坐标系 1.坐标系 过空间一定点O作三条互相垂直的数轴,它们都 以O为原点,一般具有相同的长度单位,且它们的正 向符合右手法则,这样就构成了空间直角坐标系 O-yz,O称为坐标原点,三条数轴 称为坐标轴。 x轴(横轴) y轴(纵轴) 坐标轴 2轴(竖轴)
3 第四章 多元函数微分学 第一节 多元函数 一、空间解析几何简介 (一)空间直角坐标系 1.坐标系 过空间一定点 O 作三条互相垂直的数轴,它们都 以 O 为原点,一般具有相同的长度单位,且它们的正 向符合右手法则,这样就构成了空间直角坐标系 O xyz − ,O 称为坐标原点,三条数轴 称为坐标轴。 x 轴(横轴) y轴(纵轴) 坐标轴 z轴(竖轴) z y x o
2. 坐标平面 o 20X 0 三条坐标轴中每两条坐标轴可以确定一个平面,称 为坐标平面,共有三个坐标平面 x轴、y轴确定的xoy平面 y轴、z轴确定的yoz平面 坐标平面 z轴、x轴确定的z0x平面 4
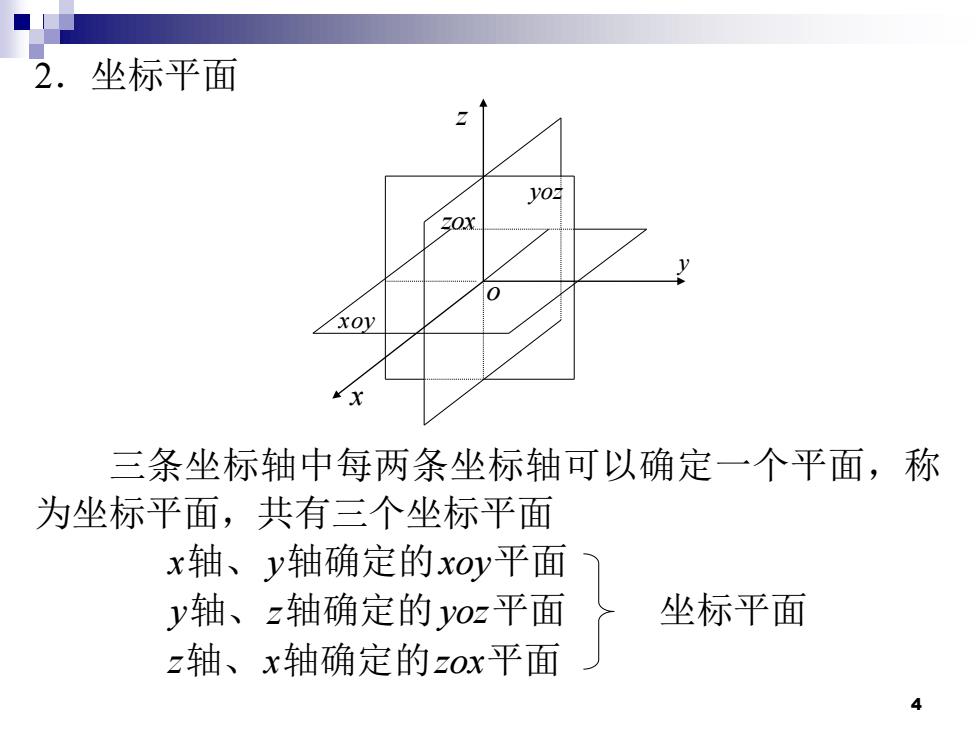
4 2.坐标平面 三条坐标轴中每两条坐标轴可以确定一个平面,称 为坐标平面,共有三个坐标平面 x轴、y轴确定的xoy平面 y轴、z轴确定的yoz平面 坐标平面 z轴、x轴确定的zox平面 o x y z xoy yoz zox
3.卦限 Ⅲ VI VI xVⅧ 三个坐标平面将空间分成八个部分,每个部分叫做卦限, 含有x轴,y轴,z轴正方向的那个卦限称为第一卦限,在xoy 平面上方,按逆时针方向,依次称为第二、第三、第四卦 限,在平面下方与第一、第二、第三、第四卦限对称地有 第五、第六、第七、第八卦限。 5
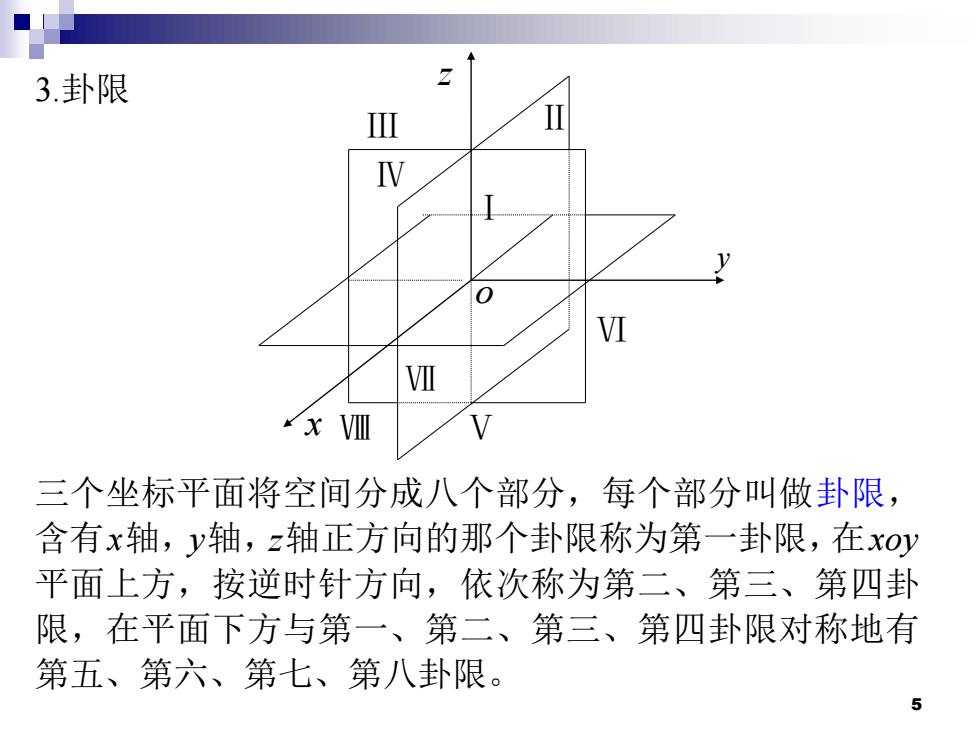
5 o x y z Ⅱ Ⅰ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ 3.卦限 三个坐标平面将空间分成八个部分,每个部分叫做卦 限, 含有x轴,y轴,z轴正方向的那个卦限称为第一卦限,在xoy 平面上方,按逆时针方向,依次称为第二、第三、第四卦 限,在平面下方与第一、第二、第三、第四卦限对称地有 第五、第六、第七、第八卦限
坐亦 P B 设P为空间一点,过P作三个平面分别垂直铲轴'轴、 二轴与它们分别交于A、B、C三点,它们往轴、y轴、2轴 的坐标分别为、y、2,于是P点唯一确定一有序数组 (x,y,z); 反之,已知有序数组(x,y,),在轴上取坐标为的点 在'轴上取坐标为'点B,在轴上取坐标为的点C,过
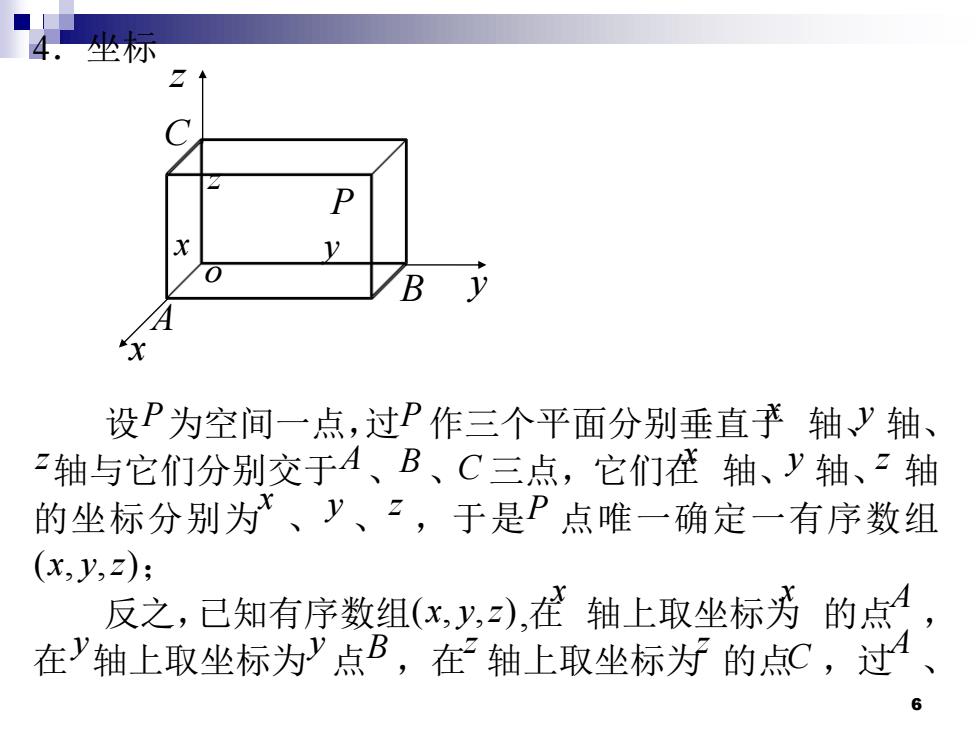
6 4.坐标 z x y 设P为空间一点,过P 作三个平面分别垂直于x 轴、y 轴、 z轴与它们分别交于A、B 、C 三点,它们在x 轴、y 轴、z 轴 的坐标分别为x 、y 、z ,于是P 点唯一确定一有序数组 ( , , ) x y z ; 反之,已知有序数组( , , ) x y z ,在 x 轴上取坐标为x 的点A , 在 y轴上取坐标为y 点B ,在z 轴上取坐标为z 的点C ,过A 、 o P B A C x y z

B、C点分别作为x轴、y轴、z轴的平面,这三个平面 交于P点,则有序数组(x,y,z)唯一确定空间的一点P。 因此,空间上一点P与一有序数组(x,y,z)建立了一 一对应关系,称(x,y,)为P点的坐标,并依次称为点的 横坐标,纵坐标,竖坐标或坐标、y坐标、2坐标。通 常记坐标为x,y,z的点P为P(x,y,z) 特殊点的坐标 坐标原点O(0,0,0) 坐标 「x轴(x,0,0) 坐标 xoy平面上(x,y,0) 轴上 y轴(0,y,0) 平面上 y0z平面上(0,y,2) 的点 轴(0,0,z) 的点 z0x平面上(x,0,2)
7 B、C 点分别作为x轴、y 轴、z 轴的平面,这三个平面 交于P点, 则有序数组( , , ) x y z 唯一确定空间的一点 P。 因此,空间上一点P 与一有序数组( , , ) x y z 建立了一 一对应关系,称( , , ) x y z 为P 点的坐标,并依次称为点的 横坐标,纵坐标,竖坐标或x 坐标、y 坐标、z 坐标。通 常记坐标为x y z , , 的点P 为P x y z ( , , )。 特殊点的坐标 坐标原点O(0,0,0) 坐标 x 轴( ,0,0) x 坐 标 xoy 平面上( , ,0) x y 轴上 y轴(0, ,0) y 平面上 yoz 平面上(0, , ) y z 的点 z轴(0,0, )z 的 点 zox 平面上( , , ) x o z