
前言 二十一世纪将是生命科学的世纪,医学科学是 生命科学的重要组成部分。 现代医学科学发展的一个显著特点是:突破了 单纯观察、描述和积累经验的传统研究方式,将现 代化实验手段与各种数学方法紧密结合起来,向着 数量化、精确化,即数学化的方向迈进。数学将象 显微镜一样帮助人们去揭示生命的奥秘。二十世纪 六十年代,生物数学的崛起,显示出数学与医学相 结合,具有强大的生命力,它不仅拓宽了医学研究 领域,也丰富了增进人类福祉的知识宝库。因此, 医用高等数学是高等医学院校各专业的必修课程。 吉林大学运程放育学院
吉林大学远程教育学院 前言 二十一世纪将是生命科学的世纪,医学科学是 生命科学的重要组成部分。 现代医学科学发展的一个显著特点是:突破了 单纯观察、描述和积累经验的传统研究方式,将现 代化实验手段与各种数学方法紧密结合起来,向着 数量化、精确化,即数学化的方向迈进。数学将象 显微镜一样帮助人们去揭示生命的奥秘。二十世纪 六十年代,生物数学的崛起,显示出数学与医学相 结合,具有强大的生命力,它不仅拓宽了医学研究 领域,也丰富了增进人类福祉的知识宝库。因此, 医用高等数学是高等医学院校各专业的必修课程。 吉林大学远程教育学院

高等数学以微积分为主线。微积分是十七世纪 自然科学最重大的发现之一。它是由英国数学家牛 顿(Isaac Newton1642-1727)和德国数学家莱布尼 兹(G.W.Leibniz,1646-1716)几乎同时发明的。微 积分的出现是由初等数学向高等数学转变的一件具 有划时代意义的大事。它不仅成为学习高等数学各 个分支必不可少的基础。而且,毫不夸张地说,不 掌握微积分就无法学习和掌握近代任何一门自然科 学和工程技术。医学作为一门自然科学也不例外。 ■ 本课程的学习内容为,第一章至第五章: 一元函数微积分学(第一章至第三章) 多元函数微积分学(第四章) (常)微分方程基础(第五章) 吉林大学远程教育学院
吉林大学远程教育学院 高等数学以微积分为主线。微积分是十七世纪 自然科学最重大的发现之一。它是由英国数学家牛 顿(Isaac Newton 1642-1727)和德国数学家莱布尼 兹(G.W.Leibniz, 1646-1716)几乎同时发明的。微 积分的出现是由初等数学向高等数学转变的一件具 有划时代意义的大事。它不仅成为学习高等数学各 个分支必不可少的基础。而且,毫不夸张地说,不 掌握微积分就无法学习和掌握近代任何一门自然科 学和工程技术。医学作为一门自然科学也不例外。 本课程的学习内容为,第一章至第五章: 一元函数微积分学(第一章至第三章) 多元函数微积分学(第四章) (常)微分方程基础(第五章)

第一章函数和极限 第一节函数 一、 函数的概念 1、实例 例1.在出生后1-6个月期间内,正常婴儿的体 重近似满足以下关系式: y=0.6x+3 式中,表示婴儿的年龄(月),表示体重(千克) 吉林大学远程教育学院
吉林大学远程教育学院 第一章 函数和极限 一、函数的概念 第一节 函数 1、实例 例1.在出生后1-6个月期间内,正常婴儿的体 重近似满足以下关系式: y = 0.6x + 3 式中,表示婴儿的年龄(月),表示体重(千克) x y
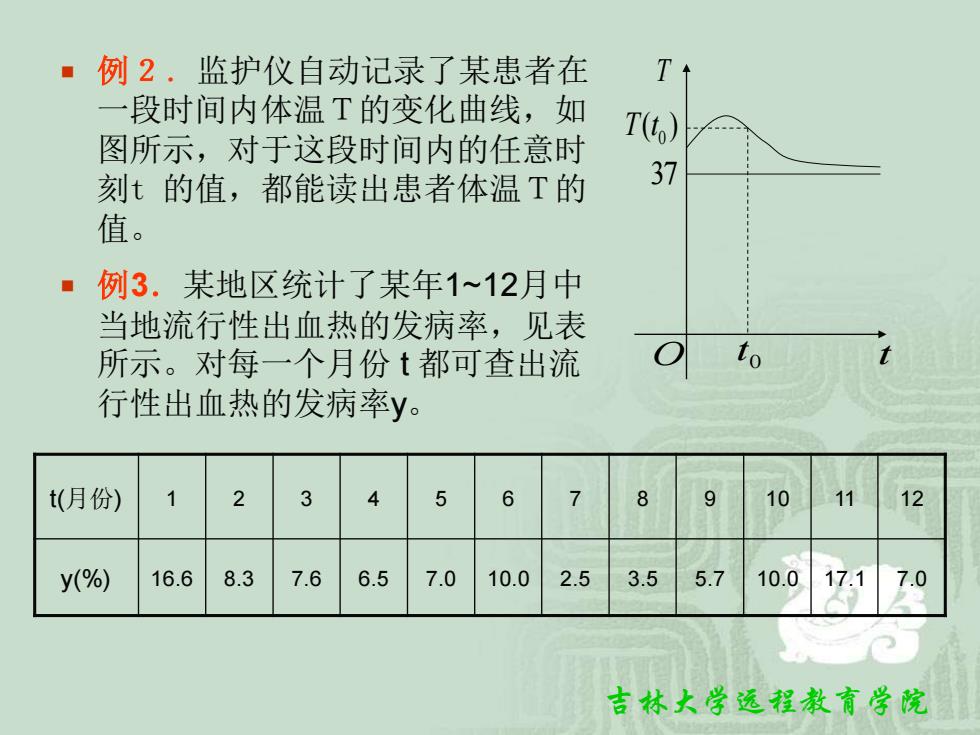
·例2.监护仪自动记录了某患者在 T 一段时间内体温T的变化曲线,如 T(t) 图所示,对于这段时间内的任意时 刻t的值,都能读出患者体温T的 37 值。 ·例3.某地区统计了某年1~12月中 当地流行性出血热的发病率,见表 所示。对每一个月份t都可查出流 to 行性出血热的发病率y。 t(月份) 1 2 4 5 6 7 8 9 10 11 12 y(%) 16.6 8.3 7.6 6.5 7.0 10.0 2.5 3.5 5.7 10.0 17.1 7.0 吉林大学远程教育学院
吉林大学远程教育学院 例2.监护仪自动记录了某患者在 一段时间内体温T的变化曲线,如 图所示,对于这段时间内的任意时 刻t 的值,都能读出患者体温T的 值。 例3.某地区统计了某年1~12月中 当地流行性出血热的发病率,见表 所示。对每一个月份 t 都可查出流 行性出血热的发病率y。 O t 0 t 370 T t( ) T t(月份) 1 2 3 4 5 6 7 8 9 10 11 12 y(%) 16.6 8.3 7.6 6.5 7.0 10.0 2.5 3.5 5.7 10.0 17.1 7.0

2、概念 定义1-1设x,y是同一变化过程中的两个变量,若对应 于变量x的每一个允许值,变量y依照某一对应规律f 总有唯一个确定的值与之对应,则称变量y是变量x的函 数。其中称x为自变量,y称为因变量。记为y=f(x)。 只有一个自变量的函数,称为一元函数。自变量的 所有允许值的集合称为函数的定义域。若x,是函数f(x) 的定义域中一点,则称函数f(x)在x点有定义,与x,对 应的因变量的值称为函数值,记为f),或记为川 所有函数值的全体称为值域。 吉林大学远程教育学院
吉林大学远程教育学院 2、概念 定义 1-1 设x, y是同一变化过程中的两个变量,若对应 于变量x 的每一个允许值,变量y 依照某一对应规律 f 总有唯一个确定的值与之对应,则称变量y是变量x的函 数。其中称x为自变量,y称为因变量。记为y f x = ( )。 只有一个自变量的函数,称为一元函数。自变量的 所有允许值的集合称为函数的定义域。若 0 x 是函数 f x( ) 的定义域中一点,则称函数 f x( )在 0 x 点有定义,与 0 x 对 应的因变量的值称为函数值,记为 0 f x( ),或记为 0 x x y = 。 所有函数值的全体称为值域