
期末考试模拟试卷(二) 一、选择题 x2-1 1.f(x)= r<1 x-1 2x x≥1 则x=1是f(x)的( ) A.连续点 B.可去间断点 C.跳跃间断点 D.无穷间断点 解f1)=2 f(1-0)=limf(x)lim x2- =lim(x+1)=2=f0 、 r 刘X-1 x→1 f(1+0)=lim f(x)=lim 2x=2=f(1) x->1 x→1 所以f(x)在x=1点处连续,x=1为连续点,故选A
3 期末考试模拟试卷(二) 一、选择题 1. 2 1 1 ( ) 1 2 1 x x f x x x x − = − , 则x =1是 f x( )的( ) A.连续点 B.可去间断点 C.跳跃间断点 D.无穷间断点 解 f (1) 2 = 2 1 1 1 1 (1 0) lim ( ) lim lim( 1) 2 x x x 1 x f f x x x → → → − − − − − = = = + = − = f (1) 1 1 (1 0) lim ( ) lim 2 2 (1) x x f f x x f → → + + + = = = = 所以 f x( )在x =1点处连续,x =1 为连续点,故选 A

2.f'(=g(x),则dfsm2x)等于() dx A.2g(x)sinx B.g(x)sin2x C.g(sin2x) D.g(sin2x)sin2x 解 么sn划=inin划 =f(sin2x)2sinxcosx =f(sin2x)sin2x =g(sinx)sin2x 故选D
4 2. f x g x ( ) ( ) = ,则 2 (sin ) d f x dx 等于( ) A. 2 ( )sin g x x B. g x x ( )sin 2 C. 2 g x (sin ) D. 2 g x x (sin )sin 2 解 2 2 2 (sin ) (sin )(sin ) d f x f x x dx = 2 = f x x x (sin )2sin cos 2 = f x x (sin )sin 2 2 = g x x (sin )sin 2 故选 D

3 3.定积分 sin2xd☑的值为( A. C.D. 解 1sn2xs-sim2d+度(←-sin2xh 3 2 故选
5 3.定积分 3 4 0 | sin 2 | x dx 的值为( ) A. 1 2 B. 1 2 − C. 3 2 D. 3 2 − 解 3 4 0 | sin 2 | x dx 3 2 4 0 2 sin 2 ( sin 2 ) xdx x dx = + − 3 2 4 2 0 1 1 cos2 cos2 2 2 x x = − + 3 2 = 故选 C

4.设函数(x)=edt,则( A.Φ(x)是单调递增函数,且其图形不过原点 B.Φ(x)是单调递增函数,且其图形过原点 C.Φ(x)是单调递减函数,且其图形过原点 D.Φ(x)是单调递减函数,且其图形不过原点 解 Φ'(x)=ex>0 故Φ(x)单调递增 (x)-fedi-0 故Φ(x)的图形过原点(0,0)。选B 6
6 4.设函数 2 0 ( ) x t x e dt − = ,则( ) A.( ) x 是单调递增函数,且其图形不过原点 B.( ) x 是单调递增函数,且其图形过原点 C.( ) x 是单调递减函数,且其图形过原点 D.( ) x 是单调递减函数,且其图形不过原点 解 2 ( ) 0 x x e − = 故( ) x 单调递增 0 2 0 ( ) 0 t x e dt − = = 故( ) x 的图形过原点(0,0) 。选 B
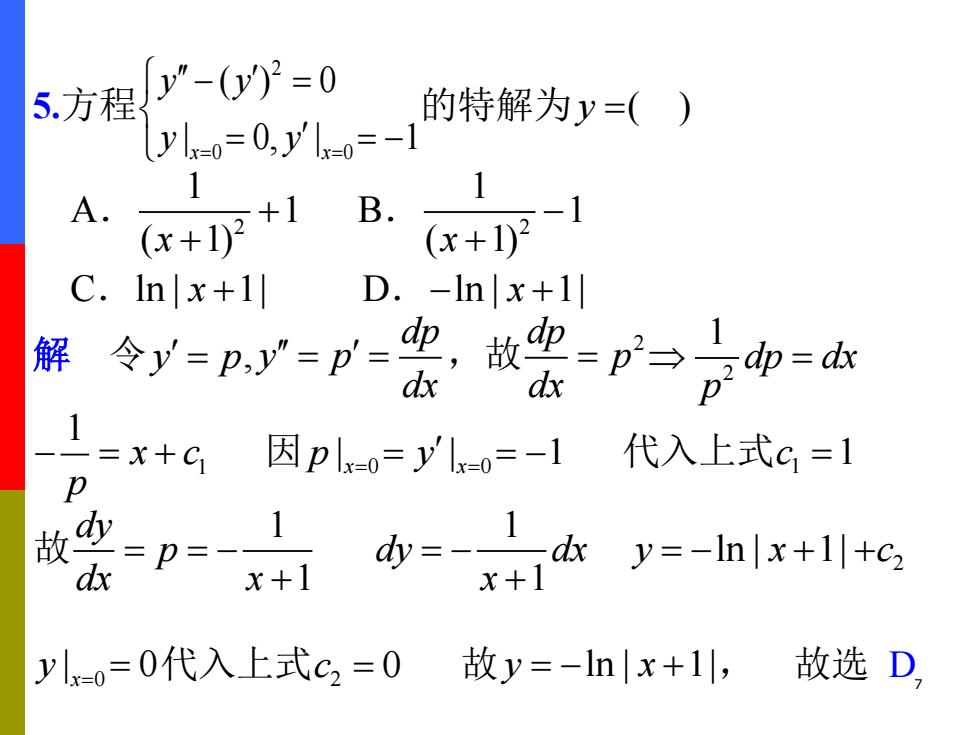
5.方程 y”-(0y)2=0 的特解为y=() yl-0=0.l-0=-1 1 A. 1 B. -1 (x+1)2 (x+1)2 C.Inx+1 D.-Inx+1 解 令y=p,y=p=中,故 dp dx dx =p2→ dx =x+c 因plx-0=ylx-o=-1 代入上式c=1 p =p=- dx x+1 ylg ylo=0代入上式c2=0 故y=-lnx+l, 故选D
7 5.方程 2 0 0 ( ) 0 | 0, | 1 x x y y y y = = − = = = − 的特解为y =( ) A. 2 1 1 ( 1) x + + B. 2 1 1 ( 1) x − + C.ln | 1| x + D.− + ln | 1| x 解 令y p = , dp y p dx = = ,故 dp 2 p dx = 2 1 dp dx p = 1 1 x c p − = + 因 0 0 p y | | 1 x x = = = = − 代入上式c1 =1 故 1 1 dy p dx x = = − + 1 1 dy dx x = − + 2 y x c = − + + ln | 1| 0 | 0 x y = = 代入上式c2 = 0 故y x = − + ln | 1|, 故选 D