
上讲提要 1.换元积分法; 2.分部积分法: 3.有理函数积分。 3
3 上 讲 提 要 1. 换元积分法; 2. 分部积分法; 3.有理函数积分
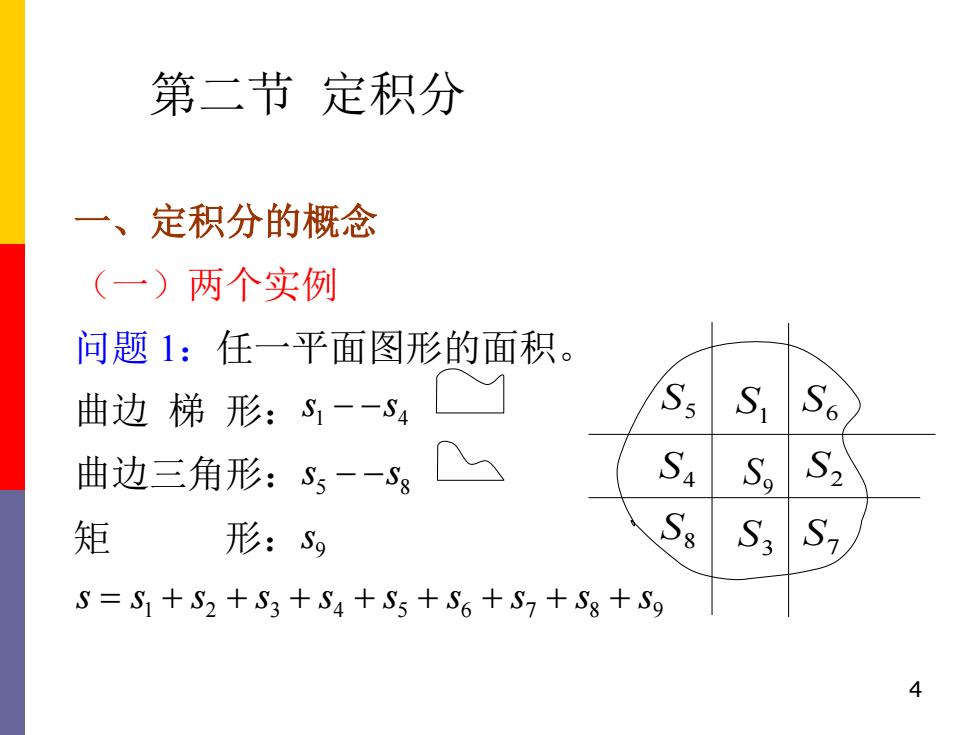
第二节定积分 一、定积分的概念 (一)两个实例 问题1:任一平面图形的面积。 曲边梯形:S,--S4 Ss S S6 曲边三角形:S--Sg So S2 矩 形:Sg Se S3 S=S1+S2+S3+S4+S5+S6+S7+S8+Sg 4
4 第二节 定积分 一、定积分的概念 (一)两个实例 问题 1:任一平面图形的面积。 曲边 梯 形: 1 4 s s − − 曲边三角形: 5 8 s s − − 9 S 矩 形: 9 s 1 2 3 4 5 6 7 8 9 s s s s s s s s s s = + + + + + + + + S2 S1 S3 S4 S5 S6 S7 S8
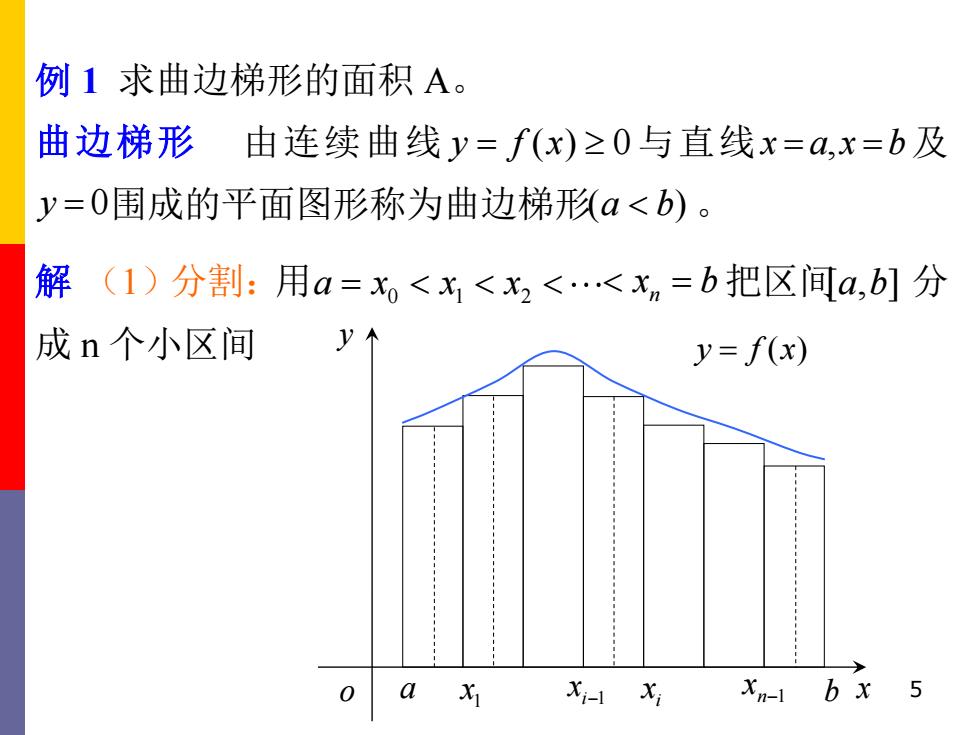
例1求曲边梯形的面积A。 曲边梯形 由连续曲线y=f(x)≥0与直线x=a,x=b及 y=0围成的平面图形称为曲边梯形队a<b)。 解(1)分割:用a=x。<x<x2<<xn=b把区间a,b]分 成n个小区间 y=f(x) a X-1 Xn-1 b x 5
5 例 1 求曲边梯形的面积 A。 曲边梯形 由连续曲线 y f x = ( ) 0与直线x a x b = = , 及 y = 0围成的平面图形称为曲边梯形( ) a b 。 解 (1)分割:用 0 1 2 a x x x = n = x b 把区间[ , ] a b 分 成 n 个小区间 y f x = ( ) y o a b x 1 x i 1 x − i x n 1 x −

[xo,],…,[x-1,x],…,[xn-1,xn]。小区间长度 △x,=x,-x1。得n个小曲边梯形面积,记为 △4,i=1,2,…,n (2)近似代替: y=f(x) V5∈[x-,x], △4≈f(5)△xi=1,2,5,n (3)求和: A=2a4f54 X-15X Xn-15nbx
6 0 1 1 1 [ , ], ,[ , ], ,[ , ] i i n n x x x x x x − − 。 小 区 间 长 度 i i i 1 x x x = − − 。 得 n 个小曲边梯形面积,记为 Ai ,i n =1,2, , (2)近似代替: 1 [ , ] i i i x x − , ( ) 1,2, , = A f x i n i i i (3)求和: 1 1 ( ) n n i i i i i A A f x = = = y f x = ( ) y o a b x 1 x i 1 x − i x n 1 x − 1 i n

(4)求和的极限 A=lm∑f(5Ay -0 其中=max{△x,} 1<i<n 问题2.变速直线运动的路程 例2.直线运动的速度v=v(t)≥0,在[T,T,]上连续, 求在时间间隔[T,T,]内物体所经过的路程S。 解(1)分割:用n+1个分点T=t<t<t,2<…<tn=T, 把区间[T,T,]分割成n个小区间 7
7 (4)求和的极限 0 1 lim ( ) n i i i A f x → = = 其中 1 max i i n x = 问题 2.变速直线运动的路程 例 2. 直线运动的速度v v t = ( ) 0,在 1 2 [ , ] T T 上连续, 求在时间间隔 1 2 [ , ] T T 内物体所经过的路程 S。 解(1)分割:用n +1个分点T t t t t T 1 0 1 2 2 = =n , 把区间 1 2 [ , ] T T 分割成n个小区间