
上讲提要 1.微元法 2.平面图形的面积、旋转体的体积 3.变力做功、连续函数的平均值 3
3 上 讲 提 要 1.微元法 2.平面图形的面积、旋转体的体积 3.变力做功、连续函数的平均值
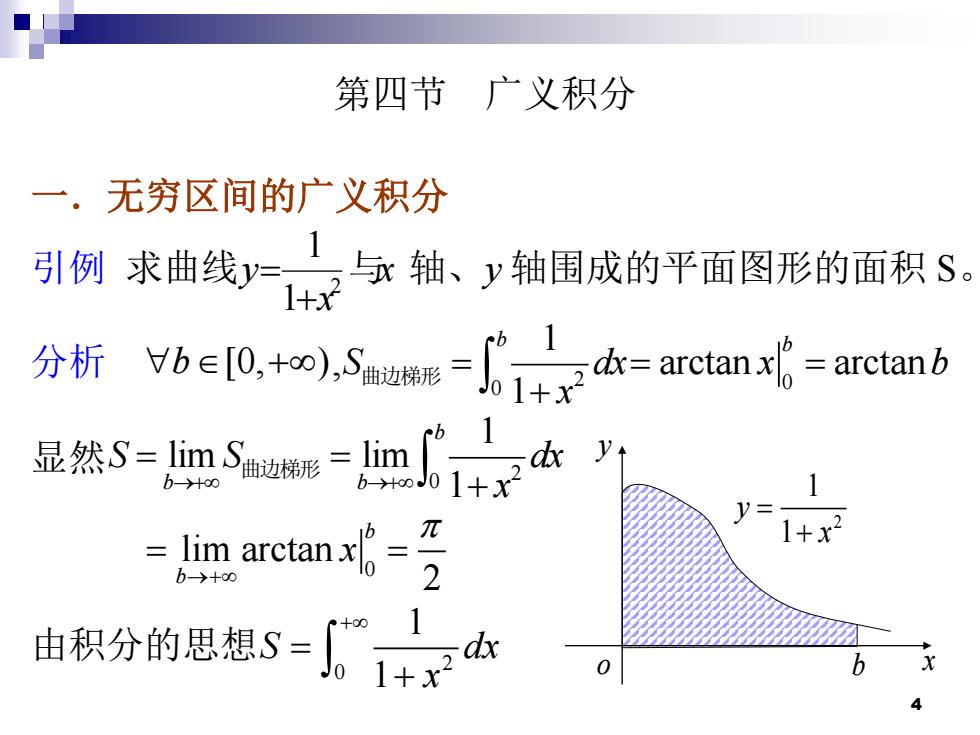
第四节广义积分 一.无穷区间的广义积分 引例求面线中轴、:箱围成的半面图形的面积S, 分析he0,+ess-1十子-c或-arean 显然s=mSe=m 6+oJ01+x V= =lim arctan x 1+x2 b→+00 由积分的思想S=1+ r+o01 。dx
4 第四节 广义积分 一.无穷区间的广义积分 引例 求曲线 2 1 1 y x = + 与x 轴、y 轴围成的平面图形的面积 S。 分析 + b [0, ), 2 0 1 1 b S dx x = + 曲边梯形 0 arctan arctan b = = x b 显然 2 0 1 lim lim 1 b b b S S dx →+ →+ x = = + 曲边梯形 0 lim arctan 2 b b x →+ = = 由积分的思想 2 0 1 1 S dx x + = + y o b x 2 1 1 y x = +

解s=4子=1本=m- 6+0J01+x 2 定义3-4设函数在区间a,+o)上连续,Hb∈[0,+oo),若极限 mf(x)d本存在,则称此极限为(x)在a,+∞)上的广义 积分,简称无穷积分,记作f(x)d,即 ∫fx)dc=lim心fax)dkr 这时也称无穷积分f(x)存在或收敛,若极限不存在, 则称无穷积分f(x)不存在或发散。 5
5 解 2 0 1 1 S dx x + = + 2 0 1 lim 1 b b dx →+ x = + 0 lim arctan 2 b b x →+ = = 定义 3-4 设函数在区间[ , ) a + 上连续, + b [0, ),若极限 lim ( ) b b a f x dx →+ 存在,则称此极限为 f x( )在[ , ) a + 上的广义 积分,简称无穷积分,记作 ( ) a f x dx + ,即 ( ) a f x dx + lim ( ) b b a f x dx →+ = 这时也称无穷积分 ( ) a f x dx + 存在或收敛,若极限不存在, 则称无穷积分 ( ) a f x dx + 不存在或发散

nf(x)=F(x)=F(+oo)-F(a),其中 F(+oo)=limF(x),F'(x)=f(x),同理 (1)无穷积分∫f(x)d=1imfx)dk亦可写为 ∫°f(x)dk=F(ax)地 (2)无穷积分f(x)d=fx)d+fx)d lim [f(x)dx+lim f(x)dx 亦可写为」f(x)d=f(x)k+∫f(x)d =F(x)+F(x) 6
6 ( ) ( ) ( ) ( ) a a f x dx F x F F a + + = = + − ,其中 ( ) lim ( ) x F F x →+ + = ,F x f x ( ) ( ) = ,同理 (1)无穷积分 ( ) b f x dx − lim ( ) b a a f x dx →− = 亦可写为 ( ) ( ) b b f x dx F x − − = (2)无穷积分 f x dx ( ) + − ( ) c f x dx − = + ( ) c f x dx + lim ( ) c a a f x dx →− = lim ( ) b b c f x dx →+ + 亦可写为 f x dx ( ) + − ( ) c f x dx − = + ( ) c f x dx + ( ) c F x − = ( ) c F x + +

例1求广义积分 解了 d=inxh"=im Inx= X)+00 放发散 X 例2求广义积分∫+本 解 arctan x+arctan x -0-lim arctanx+lim arctanx-0 X→-00 X→十00 7
7 例 1 求广义积分 1 1 dx x + 解 1 1 dx x + 1 ln x + = lim ln x x →+ = = + 故 1 1 dx x + 发散 例 2 求广义积分 2 1 1 dx x + − + 解 2 1 1 dx x + − + 0 2 1 1 dx x − = + + 2 0 1 1 dx x + + 0 arctan x − = 0 arctan x + + 0 lim arctan x x →− = − lim arctan 0 x x →+ + − 2 2 = − − + =