吉林大学：《医用高等数学》课程电子教案（PPT课件）第四章 多元函数微积分学（6/6）

上讲提要 直角坐标系下的二重积分的计算 1.D型域： fyd 2.D型域；先x后积分，即 (dd 3.交换积分次序。 fxw→f.y)da-→x冰

3 上 讲 提 要 直角坐标系下的二重积分的计算 1．Dx型域: ( , ) D f x y d  2 1 ( ) ( ) ( , ) b x a x dx f x y dy   =   2．Dy型域；先x 后y 积分,即 ( , ) D f x y d  2 1 ( ) ( ) ( , ) d x c x dy f x y dx   =   3．交换积分次序。 2 1 ( ) ( ) ( , ) b x a x dx f x y dy      ( , ) D f x y d  2 1 ( ) ( ) ( , ) d x c x dy f x y dx     

第五节 二重积分 二.二重积分的计算 (二)极坐标系下的二重积分的计算 1.二重积分极坐标系下的表示 坐标变换 x=pcos0 p(x,y) ly=psine 9 被积函数f(x,y)=f(pcos0,psin0) 面积元素 do pdpde (p,0),给0一增量d0,p一增量 dp。做射线0,0+d0做同心圆 X p,p+dp得小区域△o,并表示小 区域面积

4 第五节 二重积分 二．二重积分的计算 （二）极坐标系下的二重积分的计算 1．二重积分极坐标系下的表示 坐标变换 cos sin x y      =   = 被积函数 f x y f ( , ) ( cos , sin ) =     面积元素 d d d     = ( , )   ，给 一增量d ，一增量 d。做射线 ，  + d ；做同心圆    , + d 得小区域 ，并表示小 区域面积。 y x p x y ( , ) ( , )     x y

pp+dp do-o+dprd0-5pad0-nNna0+gpdpnd0 ≈pd pdo 故 do pdpde 所以 ∬fx,yag=J∬f(pcos8,psin8)pdpd0 5

5 1 1 1 2 2 2 ( ) ( ) 2 2 2 d d d d d d d d d                 = + − = +  故 d d d     = 所以 ( , ) ( cos , sin ) D D f x y d f d d         =      + d  d 

2. 计算方法 (1)极点在D外 过极点O做两条射线0=x,0=B使其切于D(α<B)的 边界，交点将D分成两部分，边界方程为 D=P(0) p=P(0) P(0) (p(8)<P2(0), R(0) &≤B≤B p(0)≤p≤P(0) 所以∬f,io=8.,psin0)pdp 6

6 2．计算方法 （1）极点在 D 外 过极点 O 做两条射线 = ，  = 使其切于D(   )的 边界,交点将D分成两部分,边界方程为 1    = ( ) 2    = ( ) 2  ( ) 1 2 ( ( ) ( ))      ， 1  ( ) 1 2 : ( ) ( ) D                所以 2 1 ( ) ( ) ( , ) ( cos , sin ) D f x y d d f d               =    o r

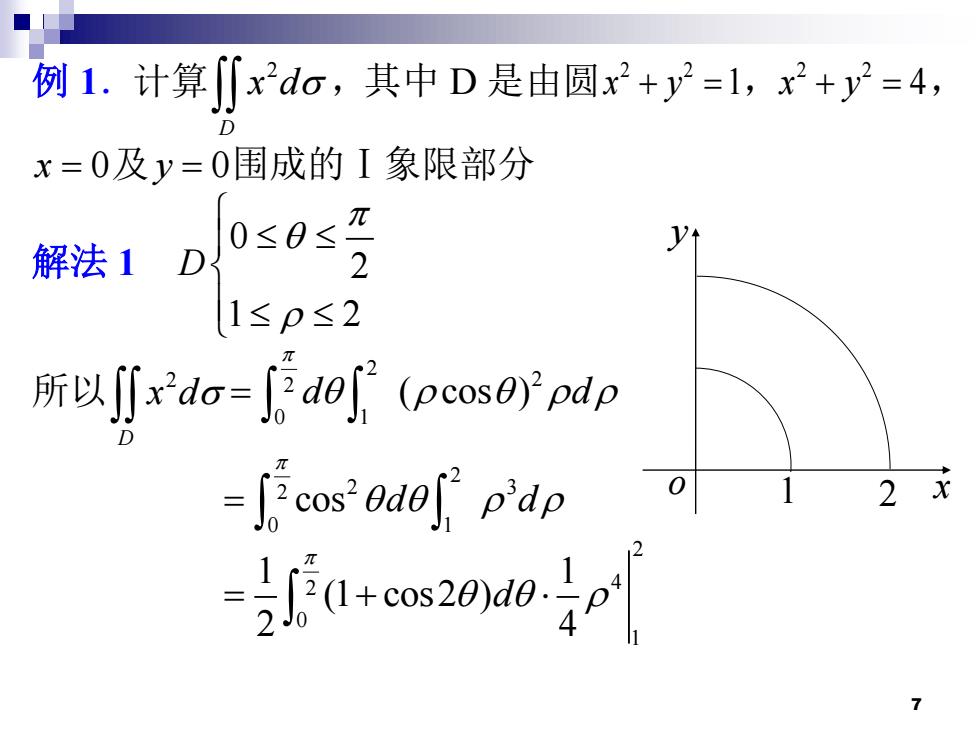
例1.计算∬x2do,其中D是由圆x2+y=1,x2+y2=4, D x=0及y=0围成的I象限部分 π 0≤0≤ 解法1D 2 1≤p≤2 所以Jj∬rdo=ao(pcos'pdp -cos'ode p'dp 号+es280d0:p 7

7 例 1．计算 2 D x d  ，其中 D 是由圆 2 2 x y + =1， 2 2 x y + = 4， x = 0及y = 0围成的Ⅰ象限部分 解法 1 0 2 1 2 D             所以 2 D x d  2 2 2 0 1 d d ( cos )  =        2 2 2 3 0 1 cos d d  =       2 2 4 0 1 1 1 (1 cos2 ) 2 4 d  = +      o y 1 2 x