
上讲提要 直接积分法 定积分的计算换元积分法 分部积分法 3
3 上 讲 提 要 定积分的计算 直接积分法 换元积分法 分部积分法

第三章 定积分的应用 一.微元法 可用条件: (1)所求量A是一个与变量x的变化区间[a,b]有关的量; (2)量A对区间具有可加性,即整体量可化成每个小区间 上的部分量之和; (3)部分量△A≈f(x)△x=f(x)dk。 基本步骤: (1)确定求的量A,由实际问题,选取一个变量x为积分 变量,并确定其变化范围[α,b]:
4 第三章 定积分的应用 一.微元法 可用条件: ⑴所求量A是一个与变量x的变化区间[ , ] a b 有关的量; (2)量A对区间具有可加性,即整体量可化成每个小区间 上的部分量之和; (3)部分量 = A f x x f x dx ( ) ( ) 。 基本步骤: (1)确定所求的量A,由实际问题,选取一个变量x为积分 变量,并确定其变化范围[ , ] a b ;

(2)x∈[a,b],给x一增量dc,(假定d>0)在[x,x+d] 上,△A≈f(x)dx,则称f(x)dx为A的微分(元),即 dA=f(x)dk。 (3)对上式积分A=∫0d4=fx)d。 二.平面图形的面积 1.y=f(x)≥0,x=a,x=b(a<b)及y=0围成的面积。 x∈[a,b],给x一增量d,在[x,x+dx]y↑ y=f(x) 上,△A≈f(x)dx,即dA=f(x)dr, 则 A=dA=f(x)d, 同理:f(x)≤0时,A=[-f(x)& xx+dx h 般情形 A=∫0f0x)1 5
5 (2) x a b [ , ] , 给 x 一 增 量 dx ,( 假 定 dx 0 ) 在 [ , ] x x dx + 上 , A f x dx ( ) , 则 称 f x dx ( ) 为 A 的 微 分 ( 元 ), 即 dA f x dx = ( ) 。 (3)对上式积分 ( ) b b a a A dA f x dx = = 。 二.平面图形的面积 1. y f x = ( ) 0,x a = ,x b a b = ( )及y = 0 围成的面积。 x a b [ , ],给 x 一增量dx ,在[ , ] x x dx + 上 , A f x dx ( ) ,即dA f x dx = ( ) , 则 ( ) b b a a A dA f x dx = = , 同理: f x( ) 0 时, [ ( )] b a A f x dx = − 一般情形 | ( ) | b a A f x dx = y o x y f x = ( ) a x x dx + b
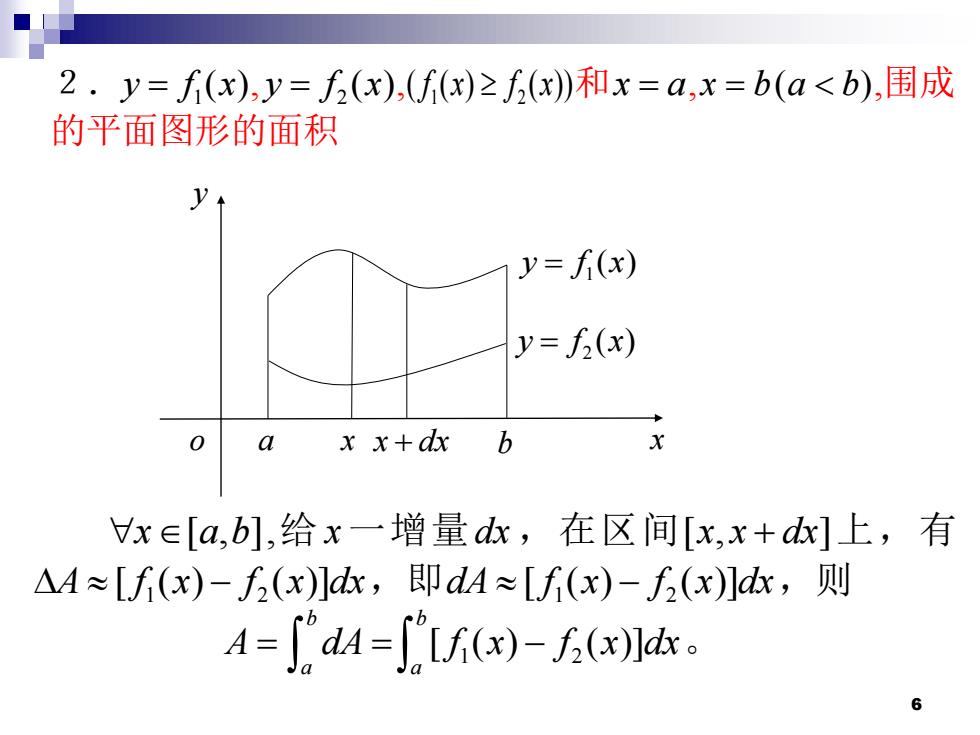
2.y=f(x),y=f(x),(f(x)≥5(x)和x=a,x=b(a<b),围成 的平面图形的面积 y=(x) y=f(x) xx+dx b x∈[a,b],给x一增量d,在区间[x,x+dx]上,有 AA≈[f(x)-f(x)]dk,即dA≈[f(x)-(x)]d,则 A=dA=Lf(x)-(xk。 6
6 2. 1 y f x = ( ), 2 y f x = ( ), 1 2 ( ( ) ( )) f x f x 和x a = ,x b = ( ) a b ,围成 的平面图形的面积 x a b [ , ],给 x 一增量dx , 在区间[ , ] x x dx + 上,有 1 2 − A f x f x dx [ ( ) ( )] ,即 1 2 dA f x f x dx − [ ( ) ( )] ,则 b a A dA = = 1 2 [ ( ) ( )] b a f x f x dx − 。 x y o 1 y f x = ( ) a x x dx + b 2 y f x = ( )

3 ·x=p(y),y=c,y=d(c<d)及x=0 围成的平面图形的面积。 y 由1的方法可得 A=@ d x=02(y) x=0(y) 4.x=0(y),x=02(y),y=C, y=d(0(y)≥p2(y),c<d)围 C 成的平面图形的面积。 x 由2的方法同理可得 A=[90)-0,0
7 3 . x y y c y d c x = = = = ( ), , ( <d) 0 及 围成的平面图形的面积。 由 1 的方法可得 ( ) d c A y dy = 4. 1 x y = ( ), 2 x y = ( ), y c = , y d = ( 1 2 ( ) ( ) y y ,c d )围 成的平面图形的面积。 由2的方法同理可得 1 2 [ ( ) ( )] d c A y y dy = − c y o x d 1 x y = ( ) 2 x y = ( )