
第四节函数的微分01微分的概念02微分的几何意义03微分的计算04微分的应用
01 微分的概念 02 微分的几何意义 03 微分的计算 04 微分的应用 第四节 函数的微分

OA问题引入实例正方形金属薄片受热后面积的改变量(x)设边长由x.变到x。xXorar口正方形面积Ax, A (x x)x)AOxiXu2x。x (x)(1)(2)(1):x的线性函数,且为A的主要部分;(2) :
问题引入 2 实例 正方形金属薄片受热后面积的改变量

OOAA问题引入再例如,函数y=x在x.点的函数增量y(x。x) x)3xx3,x)(x)(1)(2)(2)是x的高阶无穷小o(x), y 3x, x.既容易计算又是较好的近似值问题这样的线性部分(改变量的主要部分)是否所有函数的改变量都有?=lnx?如何求A?
问题引入 3 再例如, 既容易计算又是较好的近似值 问题 这样的线性部分(改变量的主要部分)是否所有函数的改变量 都有? 如何求A?

OOAA微分的概念定义2.4设函数y=f(x)在x的某邻域U(x)内有定义,x。+DxiU(x。),(2.4)若函数增量Dy=f(x+Dx)-f(x)可表示为Dy= ADx + o(Dx)其中A是不依赖于Dx的常数,而o(Dx)是比Dx高阶的无穷小,那么称函数y=f(x)在点x.是可微的.而ADx叫做函数y=f(x)在点x,相应于自变量增量Dx的微分,记作dy|x,即:dyx-=ADx.1)ADx:称为Dy的线性主部,即dy注2Dx很小时,Dy》dy若Dy=ADx+o(Dx),则称dy=ADx为函数的微分
一、 微分的概念 4 定义2.4 注
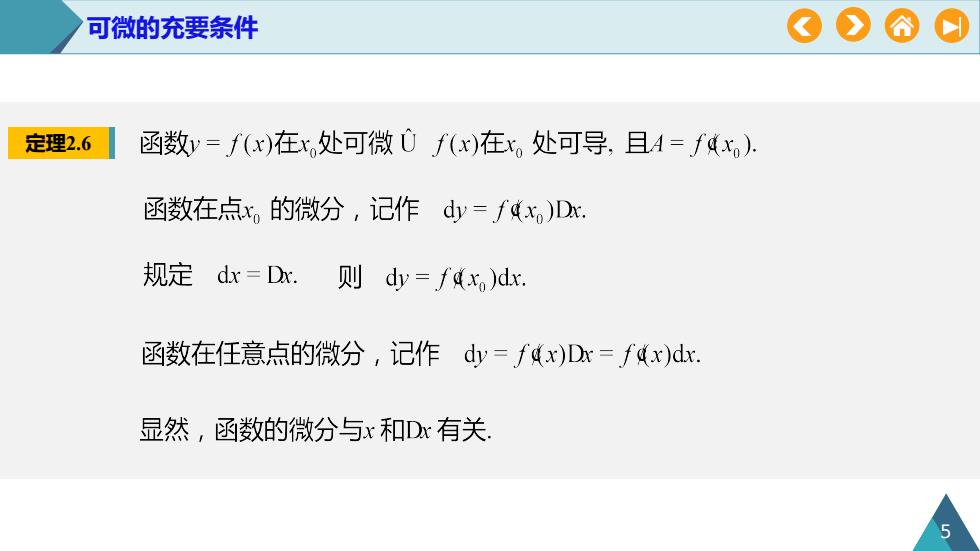
0O#0可微的充要条件定理2.6函数y=f(x)在x.处可微Uf(x)在x。处可导,且A=fdx)函数在点x。的微分,记作dy=fdx)Dx规定 dx=Dx则 dy=fdxo)dx.函数在任意点的微分,记作dy=fdx)Dx=fdx)dx显然,函数的微分与x和Dx有关5
可微的充要条件 5 定理2.6