
1.4无穷小与无穷大无穷小0102无穷大03无穷小阶的比较04等价无穷小代换
1.4 无穷小与无穷大 01 无穷小 02 无穷大 03 无穷小阶的比较 04 等价无穷小代换
COA7引入0.999...?110.999…-1]多大呢?[0.999…一11可以用实数来表示吗?像这样大于0小于任意给定正实数的量究竟是什么呢?
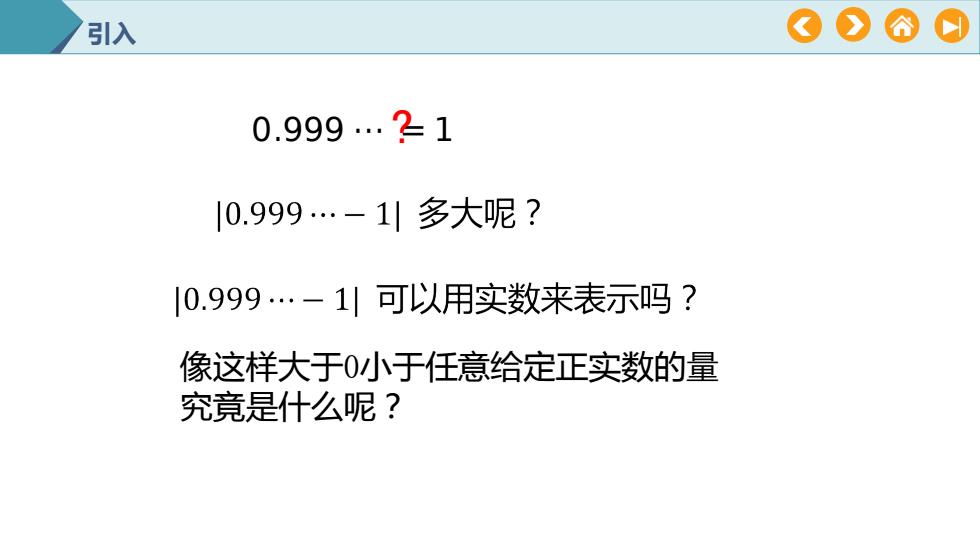
引入 0.999 ⋯?= 1 像这样大于0小于任意给定正实数的量 究竟是什么呢?

OAH一、无穷小1.无穷小的定义如果limf(x)=0,则称函数f(x)为当x?x。时的无穷小定义1.14XRX,(1)一个变量是否为无穷小,除了与变量本身有关,还与自变量的注变化趋势有关;(2)无穷小不是绝对值很小的常数,而是在自变量的某种变化趋势下,函数的绝对值趋近于0的变量.特别的,常数0可以看成任何一个变化过程中的无穷小
一、 无穷小 定义1.14 注 1. 无穷小的定义

黄鹤楼送孟浩然之广陵唐李白故人西辞黄鹤楼烟花三月下扬州。孤帆远影碧空尽唯见长江天际流

O?无穷小的发展历程公元前古希腊时代已经意识到无穷小量的存在,但穷竭法绕开了与无穷小的正面冲突。16世纪,卡瓦列里提出“面积是有无数个等距平行线段构成的,体积是有无数个平行的平面面积构成的”。他分别把这些元素称为面积和体积的不可分量。这里不可分量就是无穷小量,但当时卡瓦列里没有办法严密地说明无穷小量。17世纪,以无穷小量为基础的微积分的建立,但由于对无穷小量的解释不清,引发许多人对微积分的攻击,历史上称为“第二次数学危机”。18世纪,柯西用极限来说明无穷小量,而后由魏尔斯特拉斯给出极限的严格定义,完成了微积分体系的严密化
无穷小的发展历程 公元前古希腊时代已经意识到无穷小量的存在,但穷竭法绕开 了与无穷小的正面冲突。 16世纪,卡瓦列里提出“面积是有无数个等距平行线段构成的, 体积是有无数个平行的平面面积构成的”。他分别把这些元素称为 面积和体积的不可分量。这里不可分量就是无穷小量,但当时卡瓦 列里没有办法严密地说明无穷小量。 17世纪,以无穷小量为基础的微积分的建立,但由于对无穷小 量的解释不清,引发许多人对微积分的攻击,历史上称为“第二次 数学危机” 。 18世纪,柯西用极限来说明无穷小量,而后由魏尔斯特拉斯给 出极限的严格定义,完成了微积分体系的严密化