
实验6开普勒方程近似解与方程求根1.方程求根的Matlab指令2.“二分法”3.“牛顿切线法”4.一般迭代法5.MATLAB求方程组的近似解
1. 方程求根的Matlab指令 2. “二分法” 3. “牛顿切线法” 4. 一般迭代法 5. MATLAB求方程组的近似解 实验6 开普勒方程近似解 与方程求根

实验问题:求开普勒方程x=0.5sinx+1近似解分析:该问题可以转化为下列方程求根x- 0.5sinx- 1=0显然该方程为一元非线性方程,没有现成的求解公式6.1利用MATLAB命令求方程的近似根f=@(x)x-0.5*sin(x)-1;输出:c=1.4987c=fzero(f,[0,2])求f在区间[a,b的零点c=fzero(f,[a,b)求f在x.附近的零点c=fzero(f,xo)
实验问题: 分析:该问题可以转化为下列方程求根. 求开普勒方程 近似解. f=@(x)x-0.5*sin(x)-1; c=fzero(f,[0,2]) 6.1 利用MATLAB命令求方程的近似根 输出:c = 1.4987 显然该方程为一元非线性方程,没有现成的求解公式. c=fzero(f,[a,b]) 求f在区间[a,b]的零点 c=fzero(f,x0 ) 求f在x0附近的零点
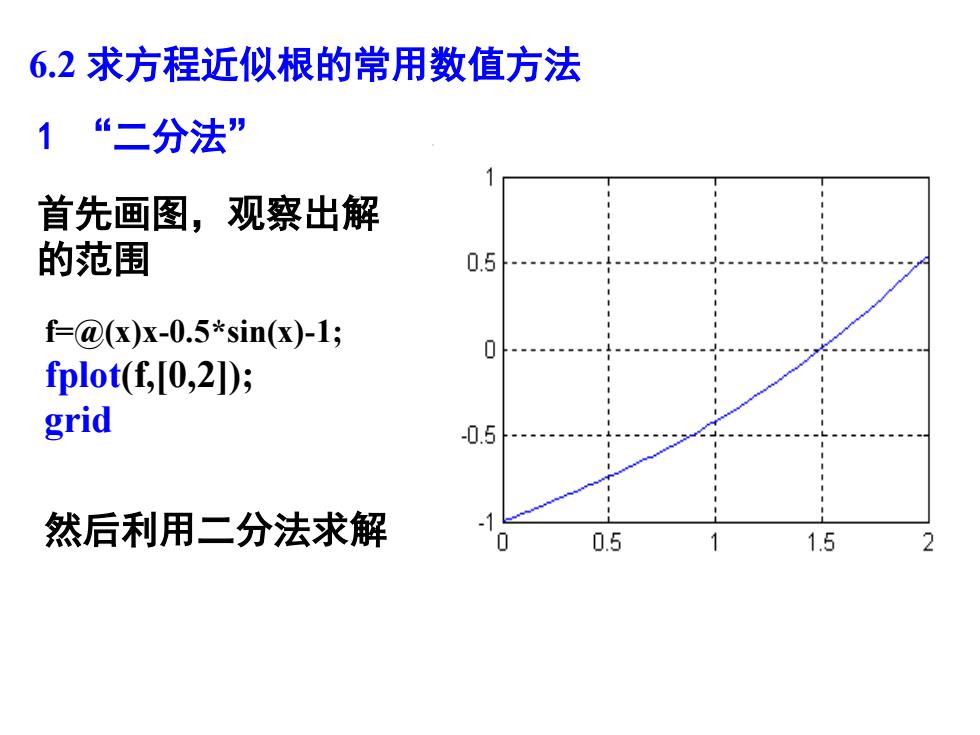
6.2求方程近似根的常用数值方法“二分法”首先画图,观察出解的范围0.5f=@(x)x-0.5*sin(x)-1;0fplot(f,[0,2D);grid-0.5然后利用二分法求解00.511.52
1 “二分法” f=@(x)x-0.5*sin(x)-1; fplot(f,[0,2]); grid 首先画图,观察出解 的范围 然后利用二分法求解 6.2 求方程近似根的常用数值方法
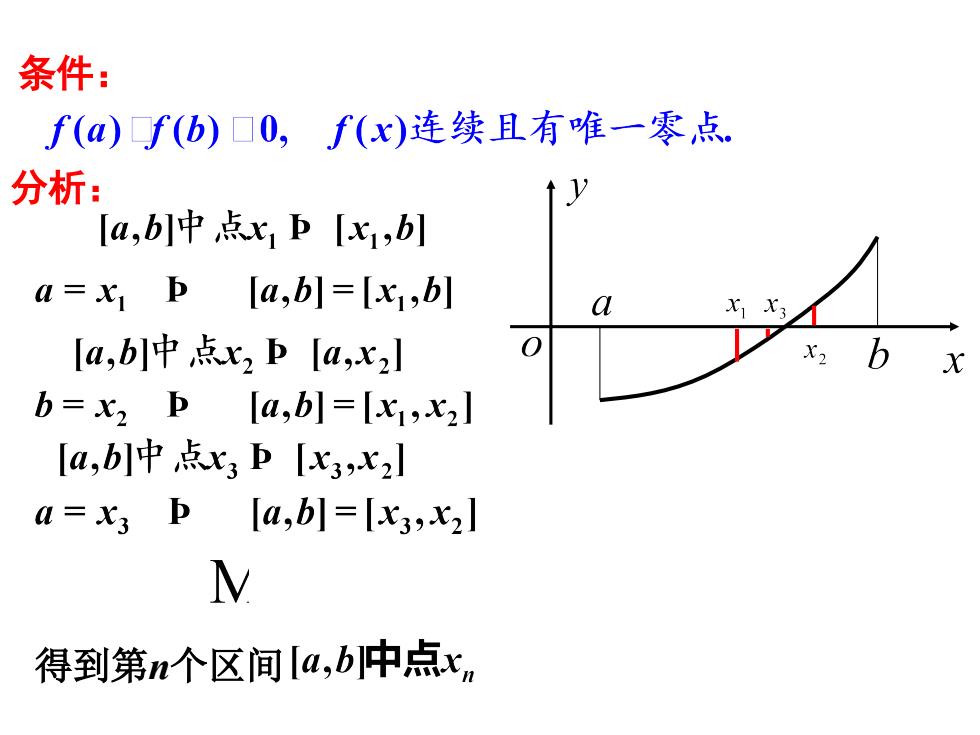
条件:f(a)f(b)0,f(x)连续且有唯一零点分析:t y[a,b]中点x, P[x,b]a=xβ[a,b]=[xj,b]aX, X30bX2[a,b]中点x, P [a,x,]xb=x, [a,b]=[xi,x,][a,b]中点x, [x3,x2]a=l[a,b]=[x3,x2]M得到第n个区间[a,b]中点x
分析: 条件: 得到第n个区间
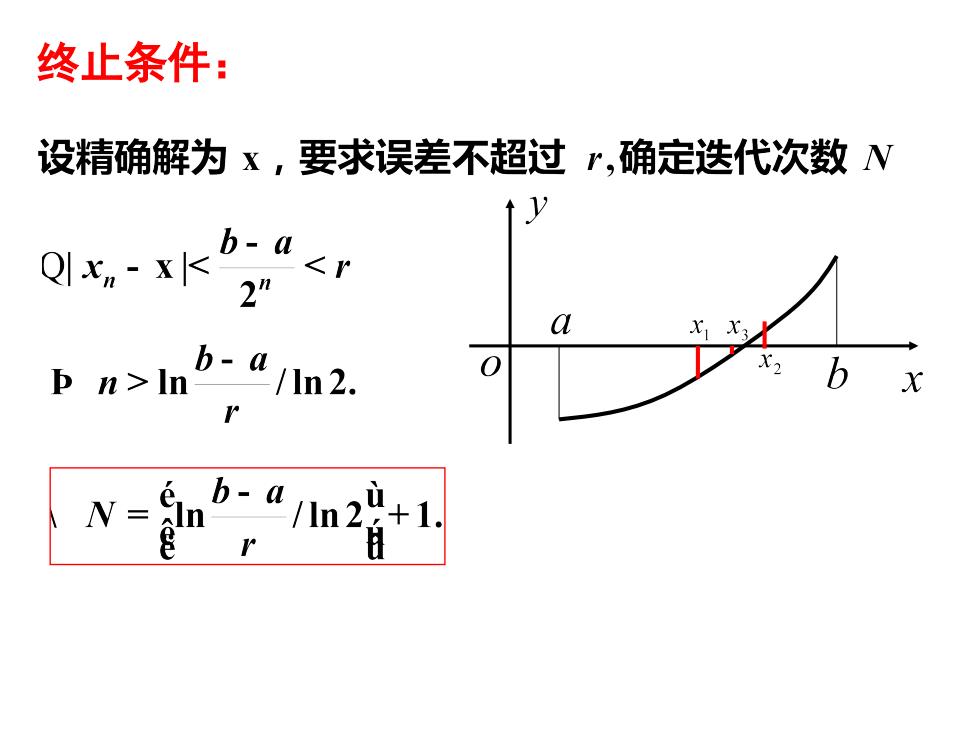
终止条件:设精确解为x,要求误差不超过r.确定迭代次数NVb-a42"aXX3b-aX20bx/ In 2.Dn >lnrb-eN+1nInee8
终止条件: