
实验8元的计算元元3.1415926535R=1897932384626433832795028841971693993751

一、圆周率元的计算历程所谓“圆周率是指一个圆的周长与其直径的比值古岑中外,许多人致力手圆周率的研究与计算。为一代代的数了计算出圆周率的越来越好的近似值学家为这个神秘的数贡献了无数的时间与心血。回顾历史,人类对,π的认识过程,反映了数学和计算技术发展情形的一个侧面。T的研究,在一定程度上反映这个地区或时代的数学水平。德国数学家康托说:“历史上一个国家所算得的圆周率的准确程度,可以作为衡量这个国家当时数学发展水平的指标。直到19世纪初,求圆周率的值应该说是数学中的头号难题。为求得圆周率的值,人类走过了漫长而曲折的道路
一、圆周率π的计算历程 v 所谓“圆周率”是指一个圆的周长与其直径的比值。 古今中外,许多人致力于圆周率的研究与计算。为 了计算出圆周率的越来越好的近似值,一代代的数 学家为这个神秘的数贡献了无数的时间与心血。 v 回顾历史,人类对 π 的认识过程,反映了数学和 计算技术发展情形的一个侧面。 π 的研究,在一 定程度上反映这个地区或时代的数学水平。德国数 学家康托说:“历史上一个国家所算得的圆周率的 准确程度,可以作为衡量这个国家当时数学发展水 平的指标。” v 直到19世纪初,求圆周率的值应该说是数学中的头 号难题。为求得圆周率的值,人类走过了漫长而曲 折的道路

实验时期基于对一个圆的周长和直径的实际测量而得出的。T=3这个数v在古代世界,实际上长期使用值。中的《圣经》最早见于文字记载的有基督教章节,其上取圆周率为3。这一段描述的事大约发生在公元前950年前后
实验时期 v 基于对一个圆的周长和直径的实际测量而得 出的。 v 在古代世界,实际上长期使用 π =3这个数 值。 v 最早见于文字记载的有基督教《圣经》中的 章节,其上取圆周率为3。这一段描述的事大 约发生在公元前950年前后
几何法时期阿基米德:科学地研究这一常数的第一个人R-1是他首先提出了一种能够借助数学过程而不是通过d=/2测量,能够把π的值精确到任意精度的方法。由此,开创了圆周率计算的圆周长大于内接正多边第二阶段。形周长而小于外切正多边形周长,据说阿基米德用到了正96边形才算出他的值域
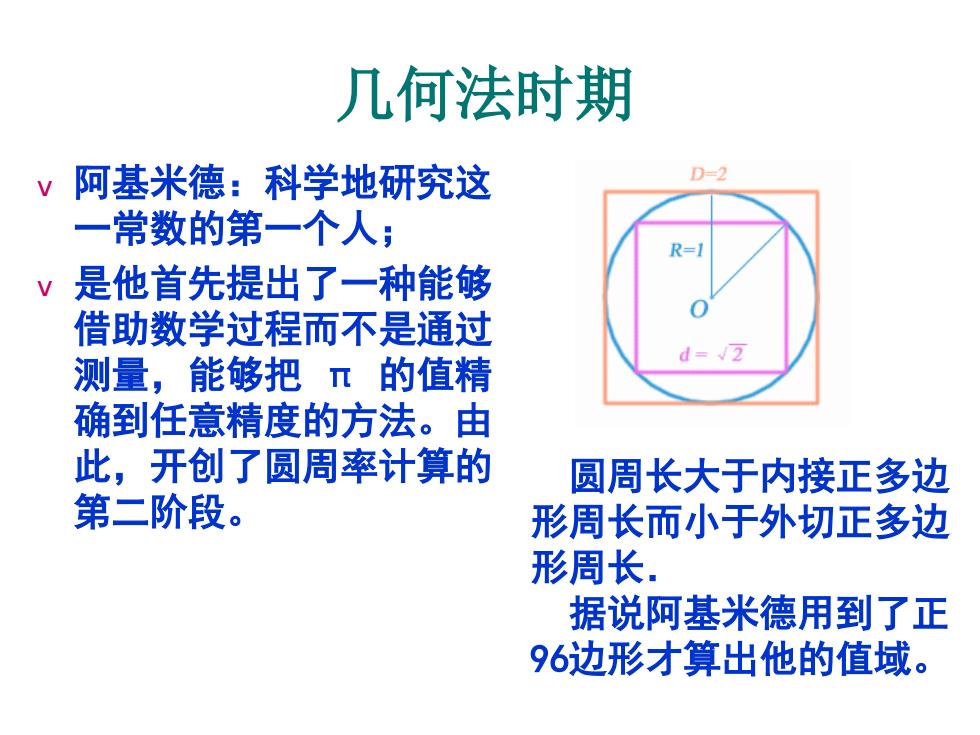
几何法时期 v 阿基米德:科学地研究这 一常数的第一个人; v 是他首先提出了一种能够 借助数学过程而不是通过 测量,能够把 π 的值精 确到任意精度的方法。由 此,开创了圆周率计算的 第二阶段。 圆周长大于内接正多边 形周长而小于外切正多边 形周长. 据说阿基米德用到了正 96边形才算出他的值域

在中国“割圆v刘徽:公元263年前后,刘徽提出著名的术”求出了比较精确的圆周率。他发现:当圆内接正多边形的边数不断增加后,多边形的周长会越来越逼近圆周长,而多边形的面积也会越来越逼近圆面积。于是,刘徽利用正多边形面积和圆面积之间的关系,从正六边形开始,逐步把边数加倍:正十二边形、正二十四边形,正四十八边形……,一直到正三○七二边形,算出圆周率等于三点一四一六,将圆周率的精度提高到小数点后第四位
在中国 v 刘徽:公元263年前后,刘徽提出著名的 “割圆 术”求出了比较精确的圆周率。他发现:当圆内 接正多边形的边数不断增加后,多边形的周长会 越来越逼近圆周长,而多边形的面积也会越来越 逼近圆面积。于是,刘徽利用正多边形面积和圆 面积之间的关系,从正六边形开始,逐步把边数 加倍:正十二边形、正二十四边形,正四十八边 形.,一直到正三○七二边形,算出圆周率等 于三点一四一六,将圆周率的精度提高到小数点 后第四位