
第二章导数与微分微积分学的创始人:英国数学家Newton德国教学家 Leibniz导数— 描述函数变化快慢微分学微分一描述函数变化程度都是描述物质运动的工具(从微观上研究函数)
微积分学的创始人: 德国数学家 Leibniz 微分学 导数 描述函数变化快慢 微分 描述函数变化程度 都是描述物质运动的工具(从微观上研究函数) 第二章导数与微分 英国数学家 Newton

① 2. 1 导数的概念①2.2函数的求导法则①2. 3隐函数及由参数方程确定的函数求导①2.4函数的微分
Ø 2.1 导数的概念 Ø 2.2 函数的求导法则 Ø 2.3隐函数及由参数方程确定的函数求导 Ø 2.4 函数的微分

2. 1 导数的概念① 一、历史背景① 二、 导数的定义① 三、 导数的几何意义口 四、可导与连续的关系
Ø 一、历史背景 Ø 二、导数的定义 Ø 三、导数的几何意义 Ø 四、可导与连续的关系 2.1 导数的概念

一、历史背景①十七世纪以来,光学透镜的设计以及炮弹轨迹的计算促使欧洲的数学家对曲线的切线进行研究;①牛顿在1761年所著《留数法和无穷级数》一书中提出的中心问题是:已知连续运动的路径,求给定时刻的速度业牛顿(1643-1727)费马(1601-1665)
一、历史背景 Ø牛顿在1761年所著《留数法和无穷级数》一书中提出的中心问题是: 已知连续运动的路径,求给定时刻的速度. Ø十七世纪以来,光学透镜的设计以及炮弹轨迹的计算促使欧洲的数 学家对曲线的切线进行研究;
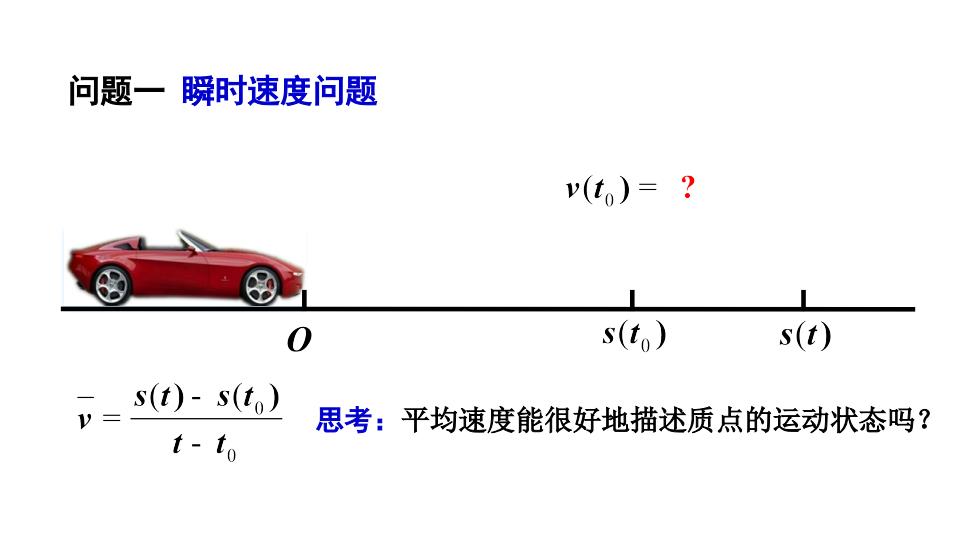
问题一瞬时速度问题v(t.) =Hs(t)s(to)0s(t) - s(to)思考:平均速度能很好地描述质点的运动状态吗?Vt- to
问题一 瞬时速度问题 思考:平均速度能很好地描述质点的运动状态吗?