
实验7Logistic方程求解与混沌
实验7 Logistic方程求解与混沌

Logistic方程与混沌在生物学中,有一个刻画生物种群个体总量增长情况的著名的方程一一逻辑斯谛(Logistic)方程:r为比例系数Xn+1 = rx,(1- xn)其中x.为某生物群体的第n代的个体总数与该群体n所能达到的最大保有量时的个体数之比选定初值和比例系数r的值后,由方程就能生成一n个数列:Xi,X2,L ,X
Logistic方程与混沌 n 在生物学中,有一个刻画生物种群个体总量增长情 况的著名的方程——逻辑斯谛(Logistic)方程: n 其中xn为某生物群体的第n代的个体总数与该群体 所能达到的最大保有量时的个体数之比。 n 选定初值和比例系数r的值后,由方程就能生成一 个数列:

考察迭代格式(Logistic方程)初值 Xx。=0.1Xn+1 = rx,(1- x,)1.当参数r取值分别为1.2,2.5,3.2,3.5,3.8考察其迭代序列的收敛情况
考察迭代格式(Logistic方程 ) 初值 1. 当参数r取值分别为1.2,2.5,3.2,3.5,3.8 考察其迭代序列的收敛情况

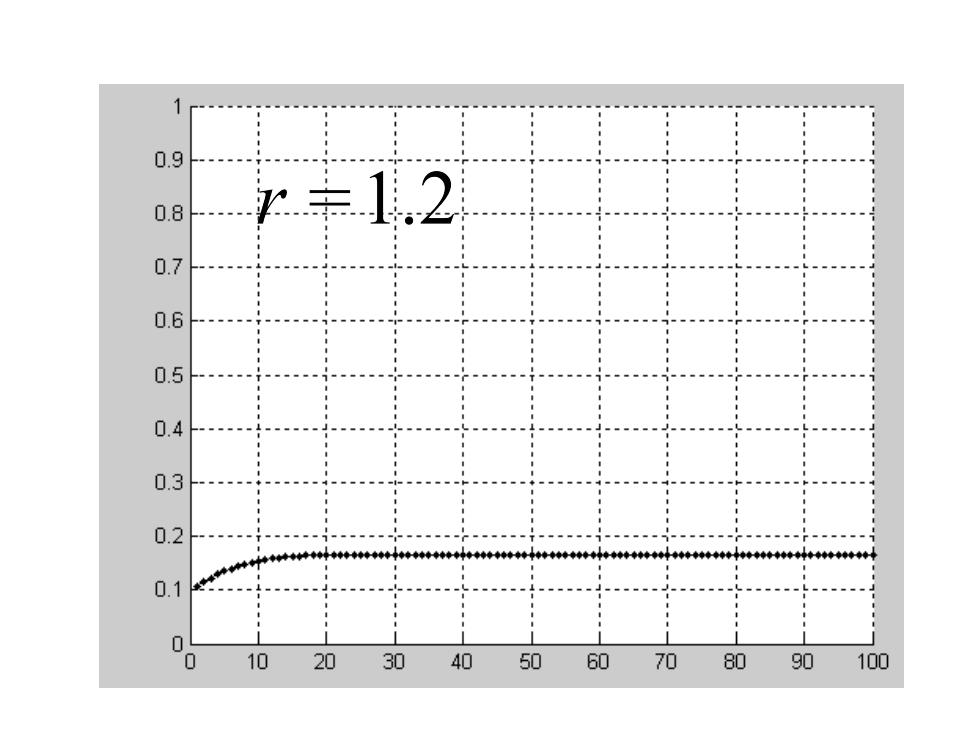
程序clc;clf;x=0.1; y=[];r=1.2;%改变取值得到相应的图形hold onaxis([0 100 0 1])for i=1:100x=r*x*(1-x);y=[y,x];plot(i,x,k.,markersize',10)fprintf(x(%d)=%.10f/n',i,x);endt=1:100;plot(t,y,'k-');grid
clc;clf; x=0.1; y=[ ]; r=1.2; %改变取值得到相应的图形 hold on axis([0 100 0 1]) for i=1:100 x=r*x*(1-x);y=[y,x]; plot(i,x,'k.','markersize',10) fprintf('x(%d)=%.10f\n',i,x); end t=1:100; plot(t,y,'k-'); grid 程序
.....--------------------------:---1-----11-I-:09r11-112---------------nV--0.8--------....1--1-11-1110.72-J--11111:--------.----...----.--1----:.I.10.6-11111.--.--------------:-------:-+-0.5----.----------------:-1111:--:---:--0.4L41.1>J1J....--------.-1:----------------0.3-.......-.....---..-....--------1:1----:--0.224oo00o0086中o809000o4008e80e042tooooooecolooocoecoolocooooecloooeooooothtjooo-----111--1-1-.0.11VLVJ1J11J----.-----...-.---------02050701030406080900100