
3.4函数的单调性、极值和最值01函数的单调性02函数的极值03函数的最值
函数的极值 函数的单调性 03 函数的最值 02 01 3.4 函数的单调性、极值和最值
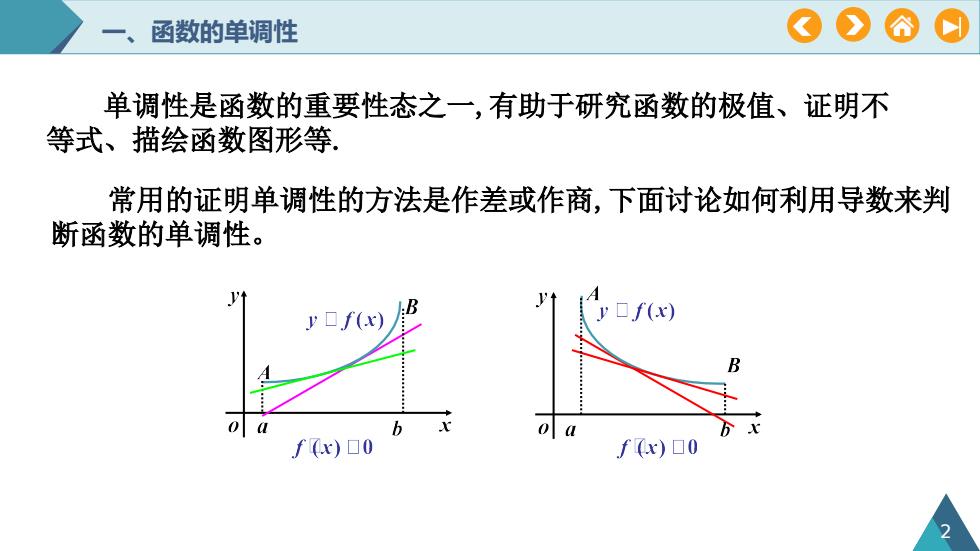
OOA0函数的单调性单调性是函数的重要性态之一,有助于研究函数的极值、证明不等式、描绘函数图形等常用的证明单调性的方法是作差或作商,下面讨论如何利用导数来判断函数的单调性。LByf(x)yf(x)B0xb0oabXf(x)0f(x)o
一、函数的单调性 2 单调性是函数的重要性态之一,有助于研究函数的极值、证明不 等式、描绘函数图形等. 常用的证明单调性的方法是作差或作商,下面讨论如何利用导数来判 断函数的单调性
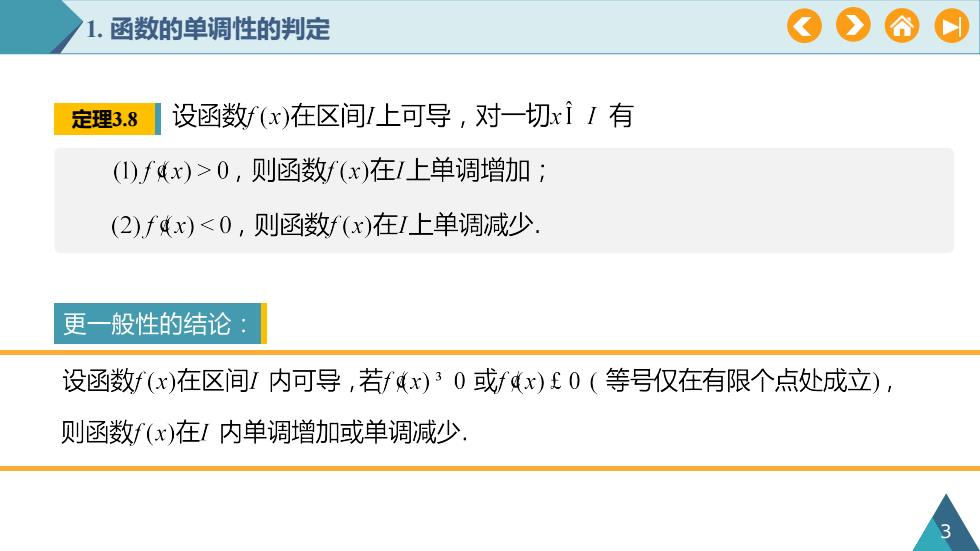
O#71.函数的单调性的判定设函数f(x)在区间/上可导,对一切xi「有定理3.8()fdx)>0,则函数f(x)在I上单调增加;(2)fdx)<0,则函数f(x)在1上单调减少更一般性的结论设函数f(x)在区间I内可导若fx)30或fdx)f0(等号仅在有限个点处成立)则函数f(x)在I内单调增加或单调减少2
1. 函数的单调性的判定 3 定理3.8

VAye1.又D:(,)解O在(,0)内, J 0,在(0,)内, J0,注:函数的单调性是一个区间上的性质,要用导数在这一区间上的符号来判定,而不能用一点处的导数符号来判别一个区间上的单调性
4 注:函数的单调性是一个区间上的性质,要用导数在这一区间 上的符号来判定,而不能用一点处的导数符号来判别一个区 间上的单调性. 例 1 解
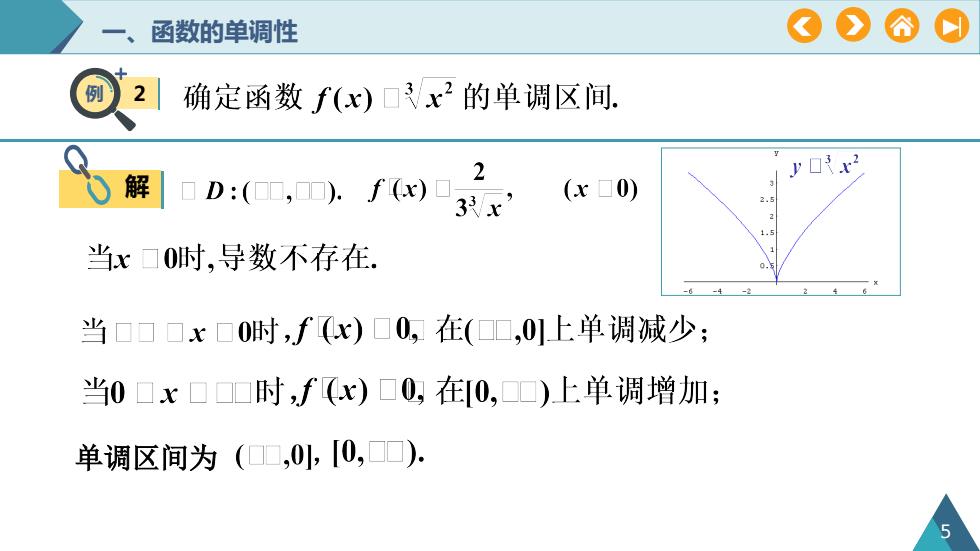
OA0函数的单调性确定函数f(x)x2的单调区间2解O(x 0) D : (,). f (x)33当x0时,导数不存在当x0时,f(x)0,在(,01上单调减少;当0x时,f(x)0,在[0,)上单调增加;单调区间为(,0],[0,)5
一、函数的单调性 5 例 2 解 单调区间为