
第三章行微分中值定理与导数的应用
第三章 微分中值定理与导数的应用
个微分中值定理(mean valuetheorem)的瞬时指导数在某个区间内所具有的一-点些重要性质,它们都与自变量区间内部的生态,某个中间值有关要用导数来研究函数的全部性态,还需架起新的“桥梁
2 因为导数是函数随自变量变化的瞬时 变 所以可借助导数来研究函数.但每一点 的导数仅仅是与局部有关的一点的变化性态, 要用导数来研究函数的全部性态,还需架起新 的“桥梁”. 微分中值定理(mean value theorem) 化率, 指导数在某个区间内所具有的一 些重要性质,它们都与自变量区间内部的 某个中间值有关
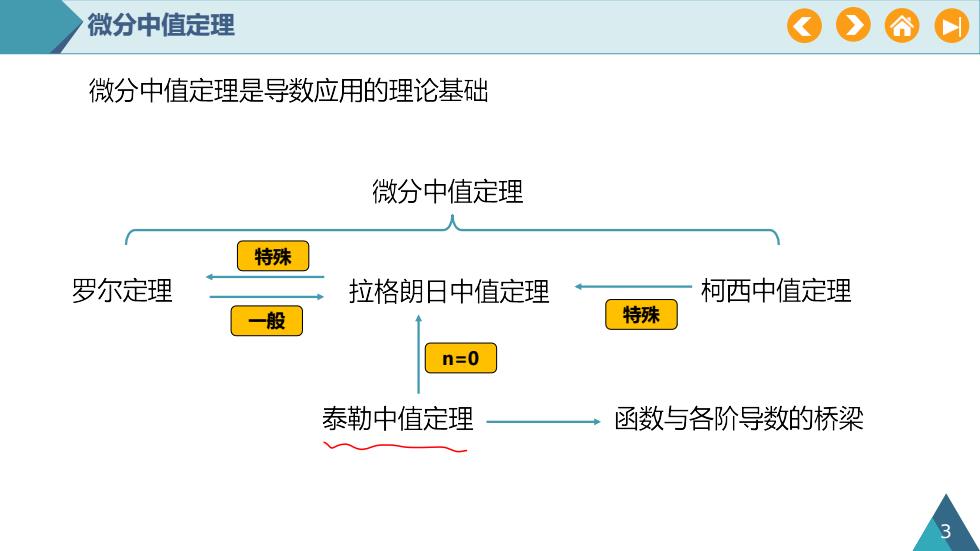
微分中值定理0OA7微分中值定理是导数应用的理论基础微分中值定理特殊罗尔定理拉格朗日中值定理柯西中值定理特殊一般n=0泰勒中值定理函数与各阶导数的桥梁
微分中值定理 3 一般 特殊 特殊 n=0
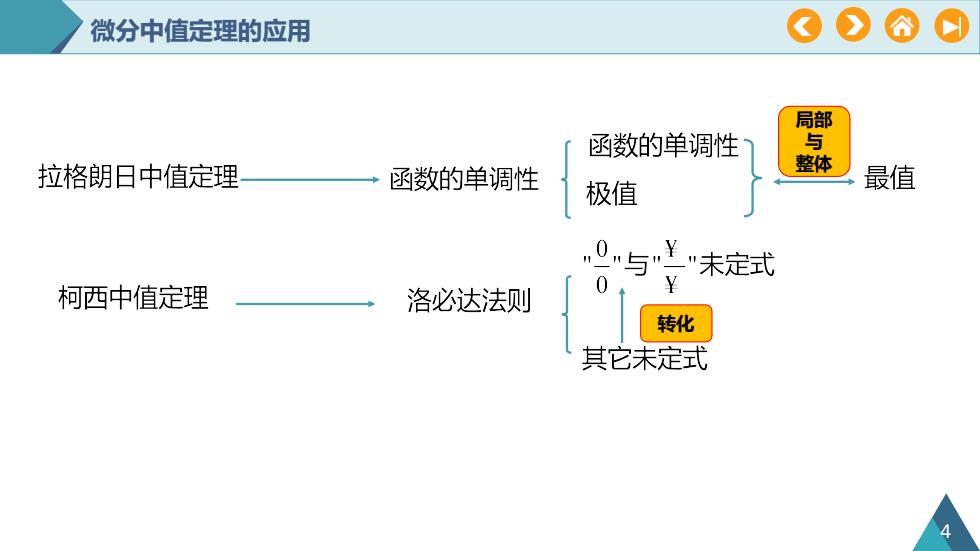
COAO微分中值定理的应用局部与函数的单调性整体最值拉格朗日中值定理函数的单调性极值¥0"未定式¥柯西中值定理洛必达法则转化其它未定式
4 局部 与 整体 转化 微分中值定理的应用

OA导数的应用增正I函数的一阶导数负减I凹正研究函数的二阶导数函数描绘函数图形负工具水平渐近线渐近线垂直渐近线斜渐近线C
导数的应用 5 研究 函数 工具 函数的一阶导数 函数的二阶导数 渐近线 正 增 负 减 正 凹 负 凸 水平渐近线 垂直渐近线 斜渐近线 描绘函数图形