
实验11缉私艇追击走私船
实验 11 缉私艇追击走私船
实验目的1(1)提高学生根据实际问题建立微分方程模型的能力;(2)学习求微分方程解析解与数值解的方法(3)学习简单的计算机仿真方法。2实验问题海上边防缉私艇发现距C公里处有一走私船正以与速沿垂直于他们连线的直线行驶缉私艇立即以最大速度追赶,在雷达的引导下,缉私艇C的方向始终指向走私船。问:缉私艇何时追赶上走私船?并求出私艇追赶的路线
1 实验目的 (1)提高学生根据实际问题建立微分方程模型的能力; (2)学习求微分方程解析解与数值解的方法; (3)学习简单的计算机仿真方法。 海上边防缉私艇发现距c公里 处有一走私船正以匀速a沿 垂直于他们连线的直线行驶, 缉私艇立即以最大速度b追 赶,在雷达的引导下,缉私艇 的方向始终指向走私船。问: 缉私艇何时追赶上走私船? 并求出缉私艇追赶的路线。 2 实验问题 c
3建立模型yy y(x)建立如图坐标系。设走私船R(0,at)初始位置在点(0,0),D(x,y)行驶方向为y轴正方向,缉私艇的初始位置在点(c, 0),0Cx缉私艇行驶的路程为S设在时刻t:缉私艇到达点D(x,J)走私船的位置到达点R(0,at),dyy-atdtdy则有xdx?x- 0dxdx2dsdt, ds = 1+(y9'dx. b.dtdxbdx o3daedy0dxédx o其中 r=a/b1 y(c) = 0, ydc) = 0
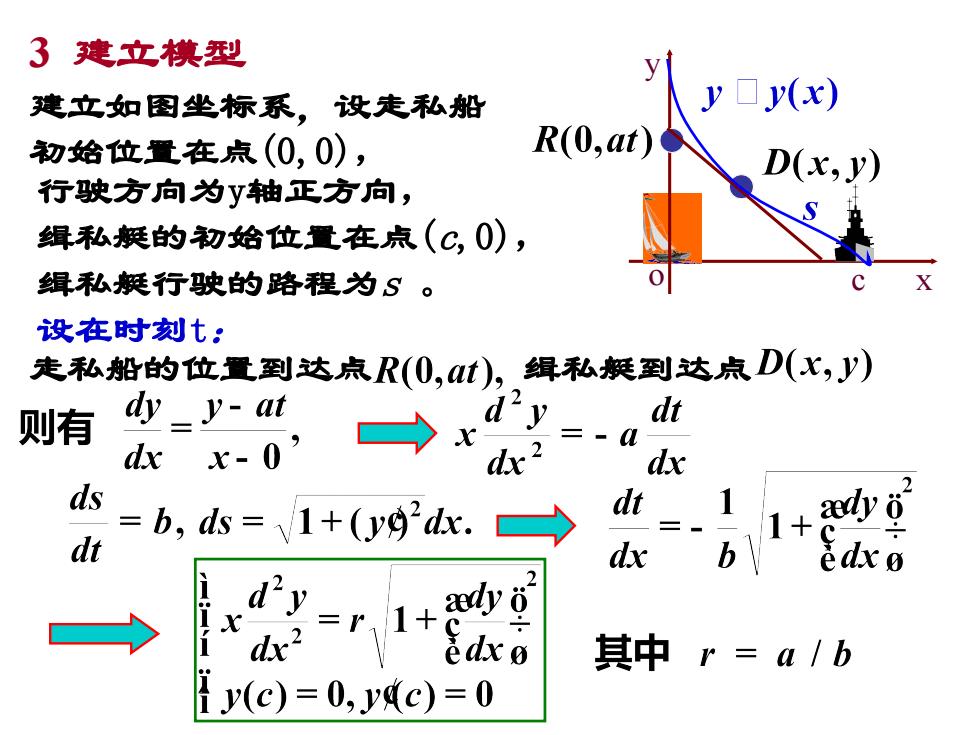
3 建立模型 o c x y 建立如图坐标系,设走私船 初始位置在点(0,0), 行驶方向为y轴正方向, 缉私艇的初始位置在点(c,0), 缉私艇行驶的路程为s 。 设在时刻t: 走私船的位置到达点 缉私艇到达点
常微分方程解析解与数值解的定义解析解:可以用数学表达式写出来的、满足微分方程的函数。数值解:由初始点X.开始的若干离散的X处的函数值25dy= f(x,y)i dx2011 y(xo) = yooOO152000Xo<Xi<X2<L <Xn108e200-00y(x,),y(x,),L (xn)58990690060909090000000.51.522.53.55013Y4.5
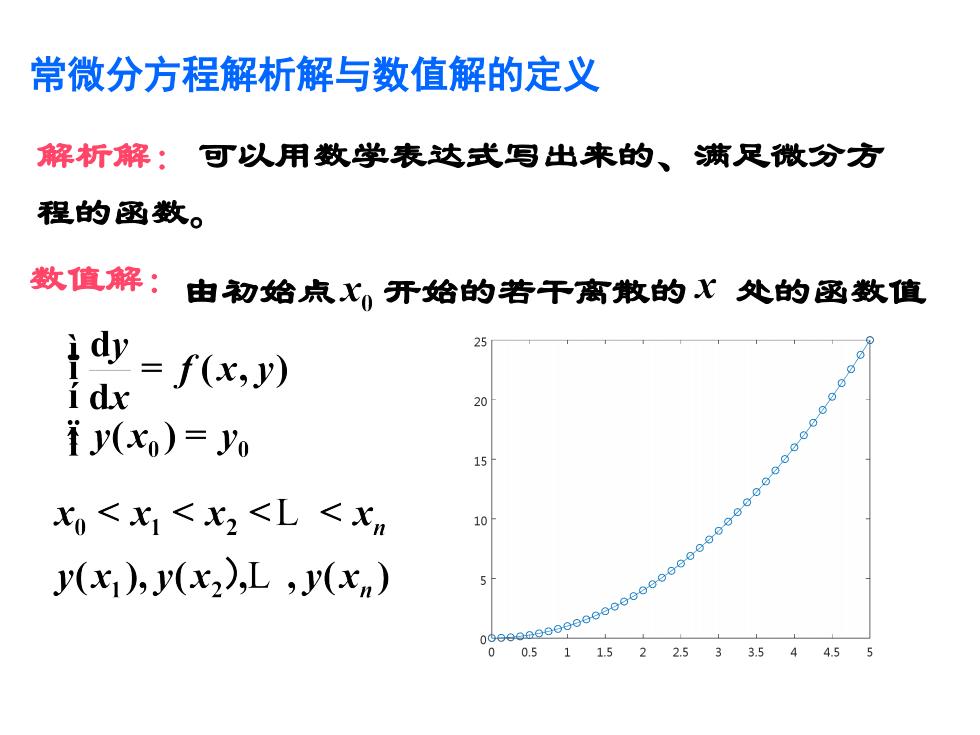
常微分方程解析解与数值解的定义 解析解: 可以用数学表达式写出来的、满足微分方 程的函数。 数值解:由初始点 开始的若干离散的 处的函数值

4 模型求解d2aedy o(1)人工求解析解Sdx odxd'ydydpy(c) = 0, ydc) = 0p,今dx?dxdx其中r=a/bdxdpa:走私船速度x/1+pb:缉私挺速度1 p(c) = 0aer o/1+pp+.aec odyécoOexoe2-.dx0aec或 p-1+p2 y(c) = 0éxo
4 模型求解 (1) 人工求解析解 令: 或