《高等数学》课程教学资源（PPT课件）第九章 多元函数微分法及其应用 9-6 第六节 多元函数微分学的几何应用

注:A= Ax(t)i+A,(t)j+A,(t)k与x = Ax(t), y= A,(t),z= A,(t)一一对应例如，已知圆柱螺旋线的参数方程x=acos0,y=asino,z=bo则其向量方程为=acosoi+asini+bok(3）向量值函数的运算法则设 A(t) = Ax(t)i + Ay(t)j+ Az(t)k并假设等式右端所遇到的运算存在

注： A = Ax t i Ay t j Az t k    ( ) + ( ) + ( ) 与x A (t), y A (t),z A (t)一一对应. = x = y = z 例如，已知圆柱螺旋线的参数方程 x = acos , y = asin ,z = b 则其向量方程为 r a cos i a sin j b k = + +    (3) 向量值函数的运算法则 A(t) = Ax t i Ay t j Az t k    设 ( ) + ( ) + ( ) 并假设等式右端所遇到的运算存在

1) lim A(t) = lim A,(t)i + lim A, (t)i + lim A, (t)kt-→>tot-→>tot-→>tot-→>to特别 lim A(t)= A(to) 称A(t)在t = t连续t-→todAdA(t),(t)dA.dA. (t)(t12)1dtdtdtdtdA(t)A(t + △t) - A(t)其中limdtdt4t->03) dA(t) = A'(t)dt i + A',(t)dt j + A'(t)dt k

0 0 0 0 1) lim ( ) lim ( ) lim ( ) lim ( ) x y z t t t t t t t t A t A t i A t j A t k → → → → = + + ( ) ( ) ( ) ( ) 2) x y z dA t dA t dA t dA t i j k dt dt dt dt = + + 特 别 lim ( ) ( 0 ) 称 ( )在 0连 续 0 A t A t A t t t t t = = →    dt A t t A t dt dA t t ( ) ( ) lim ( ) 0    + − = →   其中 3 x y z ）dA( t ) A ( t )dt i A ( t )dt j A ( t )dt k = + +   

(4）向量值函数的求导法则设i=i(t),=(t)，p(t)可导，C为常向量，则2) [Ci(t)}' = Cu'(t)1) (C)= 03) [u(t)±(t)]}' =ü(t)±(t)4) [q(t)i(t)) = p'(t)i(t) +p(t)a(t)5) [u(t) ·(t)}' = u(t) ·(t)+i(t) ·(t)6) [u(t)xi(t) =ü(t)xi(t)+i(t)x(t)) i[q(t)} = @'(t)u[q(t))

(4) 向量值函数的求导法则 设u u t v v t t C = =  ( ), ( ) ( ) ， 可导， 为常向量，则 7) [ ( )] ( ) [ ( )] u t t u t       = 2)[ ( )] ( ) Cu t Cu t   = 5 [ ( ) ( )] ( ) ( ) ( ) ( ) ）u t v t u t v t u t v t  =  +     1) ( ) 0 C  = 3 [ ( ) ( )] ( ) ( ) ）u t v t u t v t  =    4 [ ( ) ( )] ( ) ( ) ( ) ( ) ）   t u t t u t t u t    = + 6 [ ( ) ( )] ( ) ( ) ( ) ( ) ）u t v t u t v t u t v t  =  +    

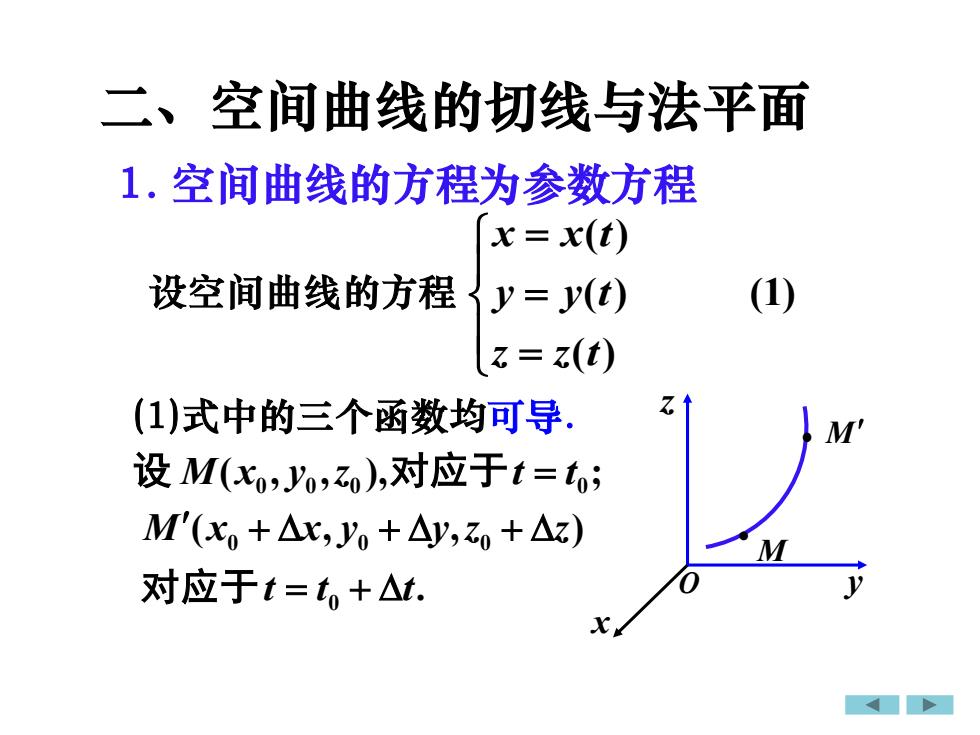
二、空间曲线的切线与法平面1.空间曲线的方程为参数方程x= x(t)(1)设空间曲线的方程y= y(t)z = z(t)Z(1)式中的三个函数均可导M'设 M(xo,Jo,z),对应于t =t;M'(x, + Axr, yo + Ay,zo + Az)My对应于t =t.+△t

设空间曲线的方程 (1) ( ) ( ) ( )      = = = z z t y y t x x t (1)式中的三个函数均可导. M • . ( , , ) 0 0 0 0 t t t M x x y y z z = +   +  +  +  对应于( , , ), ; 0 0 0 0 设 M x y z 对应于t = t • M 1. 空间曲线的方程为参数方程 二、空间曲线的切线与法平面 O x y z

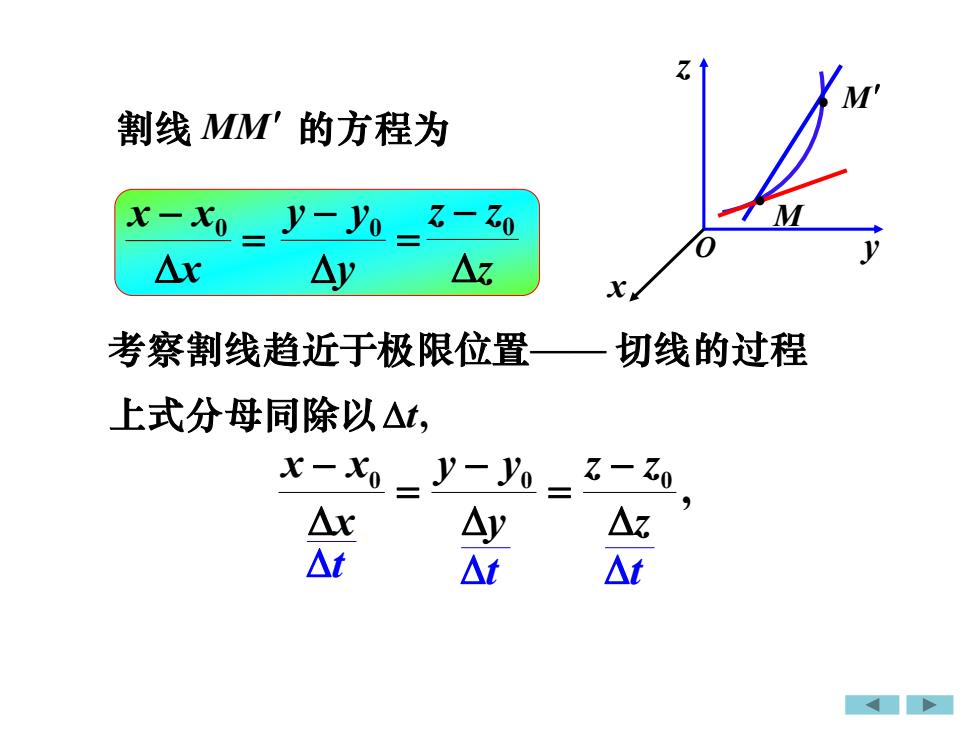
1M割线MM'的方程为M71x-xo20V-VoOyAxAzAyX考察割线趋近于极限位置切线的过程上式分母同除以△tx-xo -y- yoZ-ZoAyzAr△t△t△t

考察割线趋近于极限位置—— =  − x x x0 t t t 上式分母同除以 t, M • • M 割线 MM 的方程为 , 0 0 0 z z z y y y x x x  − =  − =  − =  − y y y0 z z z  − 0 切线的过程 O x y z